Stochastik

Beschreibung

Zur Klausur sind es nur noch 2 Tage. wie will ich mich in dieser kurzen Zeit darauf vorbereiten? In diesem Artikel nenne ich einige Lernstrategien und fasse den Stoff der Stochastik zusammen. Zuerst möchte ich einen Lernplan erstellen. Diese Lernplan sagt, was ich jeden Tag bis zur Klausur machen werde und ist präzise genug, das die anderen Klausuren wie Riemannsche und das Staatsexamen auch mit berücksichtigt werden. Ich fange dabei mit den Themengebieten an, die mir am schwersten fallen und arbeite mich dann zu den einfachen hoch. Unten stehen die verschiedenen Themen und wie gut ich die verstanden habe auf einer Skala bis 11. Am besten sollte ich versuchen schon einige Klausuraufgaben voherzusehen, indem ich bei jedem Thema, das ich bearbeite eine Beispielprüfungsfrage angebe.

Wenn man zu den Themen herunterscrollt, sieht man, dass ich die Aufgaben aus den Übungen hineinkopiert habe. An der Anzahl an Übungsaufgaben sieht man bereits, wie viel Wert Herr Deckert auf manche Inhalte legt. Ein weiterer Vorteil ist, dass ich dadurch verhindere 8 Übungsaufgaben zu einem Thema zu machen. Ich möchte smart lernen und daher ist es wahrscheinlich sinnvoll so drei Aufgaben zu machen, damit ich in dem Gebiet warm werde. Bei manchen Sachen fehlen mir noch einige Aufgaben. Das ist nicht so schlimm. Bald bearbeite ich wieder zusammen mit David und co. Klausuraufgaben. Während alle arbeiten, kopiere ich mir mal einige Aufgaben.

Aktuell habe ich ca 15 Themen zu denen ich jeweils 3 Aufgaben bearbeiten möchte. Wie in der Klausur, plane ich mir 15 Minuten pro Aufgabe ein, was eine Lernzeit von 11 Stunden ergibt. Eigentlich wäre das alles an einem einzigen Tag machbar. (Diese Einschätzung stellte sich ziemlich schnell aus unrealistisch heraus) Etwas länger vielleicht, weil ich mir die wichtigen Schlüsse einer Aufgabe auch aufschreiben will.

Bei Riemannsche Geometrie wird es ähnlich aussehen. Dort muss ich aber sogar noch die Aufgaben sammeln. Ich auch mal wieder länger schlafen.

Lernziele

Lernziele für Tag der Klausur

• Karteikarten durcharbeiten
• Die Kapitel mit niedrigem Score machen (bei den Kapiteln hängen bereits gute Aufgaben an, für die anderen kann ich mir von Matthias welche geben lassen)
• Aus der VL sind einige Sachen nachzuholen
  • Poissonscher Punktprozess
  • Statistisches Modell
  • Dominiertes Maß
  • Likelihood Funktion
  • Likelihood Quotient
  • Parameter/Schätzer
  • Erwartungstreue
  • Konsistenz
  • Konfidenzbereiche
  • Maximum-Likelihood Schätzer

Kapitel

Kombinatorik (10/11)

Am Anfang des Semesters haben wir in einigen Übungsaufgaben ein wenig Kombinatorik gemacht. Solche Aufgaben sind in Stochastikklausuren sicher gerne gesehen.

• 
• 
• Bei solchen Kombinatorischen Experimenten ohne Zurücklegen, sollte ich öfter an den Binomialkoeffizienten denken.

Modellierung & Urnenmodelle (7/11)

Wir haben die Vorlesung mit dem Einführen von Urnenmodellen begonnen.

• Der Trick bei der Aufgabe ist zu erkennen, dass es sich hier um Abbildungen $[n]\to [n]$ handelt. Die Wahrscheinlichkeit kann man kombinatorisch errechnen.

Münzwurfuniversum und Rademacherfunktionen (3/11)

David schwor, dass diese in der Klausur dran kommen werden. Ein Müzwurfuniversum ist nämlich der Prototypische Raum, mit dem Herr Deckert Zufallsvariablen einführte. Die wichtigsten Vergröberungen waren die Rademacherfunktionen, die den $k$-ten Münzwurf aus einem Universum extrahieren.

Maßtheorie (8/11)

Zu Beginn haben wir Wahrscheinlichkeitsmaße und grundlegende Definitionen aus vorherigen Semestern wiederholt. Wichtige Konzepte dieses Kapitels sind: Messraum, Sigma-Algebra, Borel-Lebesgue-Maß, Messbare Funktion, Mu-Integral.

• Diese Aufgabe ist super einfach. Man macht hier nicht viel mehr als dass man die Definitionen auflistet.
• Noch eine Aufgabe wo einfache Definitionen abgefragt werden.
• Eine sehr schöne Eigenschaft, wo man gut die Definition der Messbarkeit wiederholt. Nutzt man das Urbild der Funktionen um Messbarkeit zu zeigen, wird alles viel leichter.
• Die Aufgabe löste man, indem man die Definition des Dynkin-Systems und einer Sigma-Algebra aufschrieb und dann mir Venn-Diagrammen eine Äquivalenz zwischen Schnitt und Vereinigung konstruierte.
• Diese Aufgabe war mit einem Ven Diagramm ganz gut lösbar. Ein Trick war, das UND in ein ODER umzuwandeln nd duch abzuschätzen.

Wahrscheinlichkeiten (8/11)

Wir definieren nun einige Grundbegriffe der Wahrscheinlichkeitstheorie wie Elementarereignis, Ereignis, Ergebnisraum.

• Hier muss man clever mit Ungleichungen umgehen können. Am besten man bezeichnet die Menge aller Variablen mit gleicher Wahrscheinlichkeit als A, dann wird die Lösung hübscher.
• Hier geht man am besten vom komplizierten Term zum einfachen. Beginne einfach mit der rechten Seite und vereinfache.
• Das habe ich schon so oft gemacht. Eigentlich muss man nur alles aufaddieren und den Binomischen Lehrsatz verwenden.

Bedingte Wahrscheinlichkeiten (8/11)

Ich erinnere mich gar nicht mehr daran, dass wir das explizit in der VL behandelt hätten aber es kam im Übungsblatt dran. Ich sollte das mal lieber üben.

• Einfach alle Axiome des Wahrscheinlichkeitsraums durchgehen.

Zufallsvariablen (6/11)

Indem wir mit einem abstrakten Raum mit Gleichverteilung beginnen und von diesem auf andere Räume abbilden erhalten wir eine Möglichkeit Zufallsvariablen zu definieren. Ein prototypischer Raum, aus dem man Abbilden kann, ist das Münzwurfuniversum. Das Münzwurfuniversum können wir fast als das Intervall $[0,1]$ verstehen. Eine Gleichverteilung des Universums entspricht einer Gleichverteilung auf $[0,1]$. Mithilfe der Rademacher Funktionen können wir zwischen den Perspektiven hin und her wechseln.

• 
• Bei dieser Aufgabe ist der Trick ein doppeltes Integral zu schreiben und mit der Indikatorfunktion zu vereinfachen.

Verteilung, Dichte, Wahrscheinlichkeitsmaß (7/11)

Eine Zufallsvariable aus einem Urbildraum induziert ein Wahrscheinlichkeitsmaß auf dem Bildraum. Natürlich können wir auf dem Bildraum auch ein anderes Wahrscheinlichkeitsmaß definieren.
Hat man eine Zufallsvariable mit einem Wahrscheinlichkeitsmaß auf $\mathbb{R}$ gegeben, so kann man dessen Verteilung berechnen. Durch Ableitung der Verteilung erhalten wir die Dichte, deren Integral immer $1$ ergibt.

In der Vorlesung haben wir viele verschiedene diskrete und kontinuierliche Verteilungen kennengelernt, die formal eigentlich Dichten sind. Einige Beispiele sind Exponentialverteilung, Geometrische Verteilung, Normalverteilung, etc.

• 

Erwartungswert, Varianz & Moment (8/11)

Der Erwartungswert und die Varianz sind aus der Schule bekannt. Varianz und Standardabweichung verwechsle ich immer noch ständig aber egal. Aus der Existenz von Erwartungswert und Varianz folgen einige ziemlich wichtige Sätze. Ich sollte lernen die Werte auszurechnen.

• Diese Aufgabe habe ich gemacht und die Ergebnisse in Verteilungsfunktion zusammengefasst. Besonders bemerkenswert ist der Trick $k^2=k(k-1)+k$
• Der Trick bei dieser Aufgabe, war die Ungleichung der Verteilungsfunktion umzukehren. Schätzt man ein Minimum von oben ab, so weiß man, dass alle Werte kleiner sind. Man kann dann Unabhängigkeit nutzen und den Term in ein Produkt umschreiben.
• Diese Aufgabe hatte es ziemlich in sich. Erst erkannte man, dass man $Y_n$ als Summe von Poissonverteilten $X$ schreiben kann. Durch das starke Gesetz der großen Zahlen erhält man dann eine Konvergenz. Der nächste Trick ist, dass man unter bestimmten Umständen (z.B. dominierte Konvergenz) den Erwartungswert und den Limes vertauschen kann. Wichtig ist ebenfalls zu wissen, dass man bei stetigen Funktionen grundsätzlich den Limes nach innen ziehen darf.
• Das ist eine nette kleine Aufgabe für Zwischendurch. Wenn man gut Poisson-Verteilungen erkennen kann, löst sich die wie von ganz alleine.
• Bei dieser Aufgabe musste man wissen, dass bei unabhängigen Variablen der Erwartungswert unter Multiplikation verträglich ist. Es hat außerdem geholfen, die Terme einzeln statt auf einmal zu berechnen. Außerdem war es echt hilfreich, den Erwartungswert und Varianz der Exponentialverteilung zu wissen.

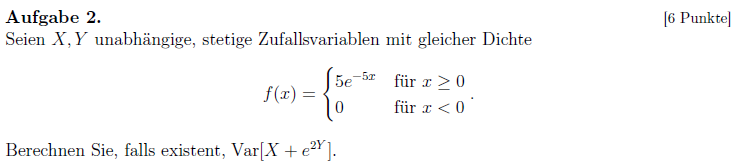
Korrelation, Kovarianz und Unabhängigkeit (4/11)

Beeinflusst eine Zufallsvariable den Wert einer anderen nicht, so sind die beiden Unabhängig. Beeinfluss die Größe einer Zufallsvariable nicht die Größe einer anderen, so sind die beiden unkorrelliert. Des Weiteren existiert noch eine Kovarianz (Stochastik) die etwas anderes macht.

Die drei Begriffe sind wichtig für die Formulierung verschiedener Sätze.

• Schöne Aufgabe, um Gegenbeispiele zu nennen.
• Bei der Unabhängigkeit von Zufallsvariablen habe ich noch einige Probleme.
• 
• 
• 

Borel-Cantelli-Lemma (7/11)

Das Borel-Cantelli-Lemma trifft eine Aussage für spezielle Ergebnisse mancher unendlich oft wiederholter Experimente. Ich weiß nicht, wo ich es sonst einteilen soll, daher ist es nun hier.

• Diese Übungsaufgabe lehrte mich, dass ich auf jeden Fall noch besser Borel Cantelli lernen muss. Ich erfuhr außerdem, dass man auf limsups achten sollte. Hier ist die Summer beispielsweise immer dann unendlich, wenn der limsup der Indikatorfunktionen 1 ist.
• Die Teilaufgabe a) war etwas gemein. Die Idee war hier, die Varianz als erwartete Abweichung zu schreiben. Ich finde, das nicht sonderlich formell aber was solls. Für die Teilaufgabe b) haben wir die unabhängigen Ereignisse $X_n\ge x$ betrachtet. Mit Borel-Cantelli konnte ich dann schließen, dass die Verteilungsfunktion überall entweder 0 oder 1 ist. Sehr schlau.
• 

Abschätzungen (7/11)

Mit der Exponentielle Tschebyscheff-Ungleichung und der Markow Ungleichung kann man Wahrscheinlichkeiten leicht abschätzen.

• Hier muss man die zweite Markow-Ungleichung anwenden, um eine Abschätzung zu erhalten, die gegen null konvergiert.

Grenzwertsätze (8/11)

Der wichtigste Grenzwertsatz ist wohl der Zentraler Grenzwertsatz. Es gibt allerdings auch stärkere Formen, die zu einfachen Lösungen führen können. So ist beispielsweise das schwache Gesetz der großen Zahlen gut geeignet, um schnell Abschätzungen zu erhalten. Eine gute Aufgabe hierzu findet man in der Altklausur von 2005

• 

Konvergenz von Verteilungen (6/11)

Sei $X$ eine reellwertige Zufallsvariable mit Erwartungswert und Varianz. Wir wiederholen das Experiment $n$ mal und betrachten den Durchschnittswert ${\hat{X}}_n=\sum ...$ Das Starkes Gesetz der großen Zahlen besagt, dass $\hat{X}$ fast sicher gegen $E(X)$ konvergiert. Das Schwaches Gesetz der Großen Zahlen besagt, dass die Wahrscheinlichkeit dafür, dass ${\hat{X}}_n$ gegen einen Wert konvergiert, der weiter als $\epsilon$ von $E(X)$ entfernt ist, gegen null geht. Der Zentraler Grenzwertsatz besagt, dass ${\hat{X}}_n$ gegen die Normalverteilung konvergiert.

Auf eine Weise, die ich noch nicht ganz begriffen habe, verallgemeinern sich diese Gesetze zu Konvergenzen.

• Die Teilaufgabe ist auf jeden Fall zu schwer für eine Klausur. Ein guter Tipp, den ich aber gesehen habe ist, dass man Ereignisse durch etwas größere Ereignisse abschätzen lässt. Am besten haben diese Ereignisse eine gegen 0 kleiner werdende Struktur. Dies erlaubt uns mit Monotonie von Sigma-Algebren zu argumentieren, dass Ereignisse fast sicher wegen der Konvergenz aus der Menge herausfallen. (Falls ich Zeit finde, könnte ich die Aufgabe nochmal). In der darauffolgenden Aufgabe fand ich heraus, dass stetige Funktionen nach Definition Grenzwerte erhalten
• 
• 

Faltung (7/11)

Addieren wir zwei reelle Zufallsvariablen, so erhalten wir eine Zufallsvariable deren Dichte die Faltung der Dichte der beiden Zufallsvariablen ist.

• 
• 

Berry-Esseen (8/11)

Dem Zentralen Grenzwertsatz zufolge konvergiert jedes wiederholte Experiment gegen eine Normalverteilung. Selbst bei vielen Versuchen ist aber ein Fehler zu erwarten. Dieser Fehler kann durch den

• Uff, diese Aufgabe hat mich mehrere Stunden gebraucht. Man muss hier echt auf zu viele Sachen aufpassen. Beispielsweise sollte man alle wichtigen Werte am Anfang als Dezimalzahlen aufschreiben. Dann berechnet man einfach die Wahrscheinlichkeit $P(\sum _{i=1}^n{X}_i\le 700)$ aus. Durch Gleichungsumformungen in der Klammer ändert sich die Wahrscheinlichkeit nicht aber man kann die Gleichung in eine hübschere Form bringen, nämlich $P(\frac{1}{\sqrt{n}\sigma }\sum _{i=1}^n{X}_i-\mu \le \frac{700-n\mu }{\sqrt{n}\sigma })$. Das links konvergiert direkt gegen die Standardnormalverteilung, weshalb man die Wahrscheinlichkeit mit dem Integral über die Standardnormalverteilung idealisiert.

Andere Verteilungen (8/11)

In der Klausur werden als Rechenbeispiele viele Verteilungen wie Geometrische Verteilung, Normalverteilung Binomialverteilung, Gleichverteilung, Exponentialverteilung, Poisson Verteilung drankommen. Falls man in der Klausur für diese einen Erwartungswert, Varianz, Charakteristische Funktion berechnen muss, wäre es nicht, dumm, das schon mal gemacht zu haben. Ich habe eine Seite erstellt, wo ich alle Eigenschaften von verschiedenen Verteilungen notiert habe. (Siehe Wahrscheinlichkeitsdichte). Mir ist aufgefallen, dass ich immer noch nicht alle Sachen weiß.

Charakteristische Funktionen (7/11)

Die charakteristische Funktion ist eine Fouriertransformation (Stochastik). Sie wird genutzt, weil viele Probleme in der Fourrierwelt einfacher zu lösen sind. Beispielsweise kann man damit Faltungen untersuchen, indem man die Charakteristische Funktion der Addition betrachtet und feststellt, dass diese wieder eine charakteristische Funktion ist.

• Mir ist aufgefallen, dass ich sehr gut darin bin, charakteristische Funktionen zu berechnen. Allerdings kenne ich noch alle Verteilungen so gut. Besonders die Poisson-Verteilung macht mir Probleme. Es wäre vielleicht gar nicht so dumm, eine Tabelle von allen Verteilungen anzufertigen. Ich probiere die Aufgabe mal mit der geometrischen Verteilung.

lausur

Aufgaben

Aufgabe 1

Bei Aufgabe a) sollte man einen Wahrscheinlichkeitsraum für das Experiment modellieren. Ich habe bei der Aufgabe nicht ganz verstanden, wie eine Modelle funktionieren. Ich sollte mir die Lösung ansehen. Bei der b) kann ich ehrlich gesagt keinen Fehler erkennen. Wenn da ein Fehler ist, dann ein Flüchtigkeitsfehler. Ich sollte aber anscheinend immer eine Argumentation mir angeben. Ich gebe mir selbst insgesamt 8/11 Punkte auf die Aufgabe statt 5/11.

Aufgabe 2

a) Vergessen monoton steigend zu prüfen. (Wäre bloß eine Ableitung gewesen). Dummer Flüchtigkeitsfehler. b) Wegen der a) fehlen mir auch zwei Punkte in b). $\lambda$ muss natürlich negativ sein c) Die Dichtefunktion erhält man nur dann durch Ableitung aus der Verteilungsfunktion, wenn die Verteilungsfunktion stetig ist. Ehrlich gesagt weiß ich nicht, wie ich das wissen sollte. Vielleicht hätte geholfen, Aufgabenbearbeitungen mit den Lösungen zu vergleichen. Falls so etwas jemals in der Lösung auftauchen sollte, hätte ich es mir für die Klausur gemerkt. So wie ich Jago kenne, hat er es außerdem sicher in seiner Übung erwähnt. Seine Übung generell scheint sehr wichtig zu sein.

Ich gebe mir 16/17 Flüchtigkeitsberichtigte Punkte.

Aufgabe 3

Aufgabe 3 war ein bisschen komisch. Bei der c) hätte ich einen liminf verwenden können. Ich warte auf die Lösung und vergleiche es dann mit ihr. Vielleicht wäre mir auch diese Aufgabe leichter gefallen, wenn sie mal in der Übung angesprochen worden war. Ich bin gerade zu faul, um mir die d) anzusehen. Ich vergleiche es später mit der Lösung. Auf jeden Fall habe ich hier eine Menge Punkte fallengelassen. Was mir hier gefehlt hat, war ein Verständnis von Borel-Cantelli. Ich habe es formal gelernt, was mir zwar bei der Definition geholfen hat aber nicht bei der Anwendung. Hier hätte ein Buch weitergeholfen, das mir eine Intuition gibt. (10/14)

Aufgabe 4

Die Aufgabe 4b) und c) war einfach nur eine Katastrophe. Ein dummer Flüchtigkeitsfehler, bei dem ich den Erwartungswert falsch ausgerechnet habe, kostete mich 9 Punkte. Ich bin mir sicher, ich hätte die Aufgabe sonst lösen können.

Dass da irgendwas nicht stimmt ist absolut offensichtlich. So nutzte ich beispielsweise nicht den in der Aufgabenstellung der c) verwendeten Tipp.

Selbst, wenn ich den Erwartungswert korrekt berechnet hätte, könnte die Aufgabe schwierig sein. Daher gebe ich mir mal keine Flüchtigkeitspunkte. (3/12 (auffwärts))

Aufgabe 5

Bei der Aufgabe habe ich einfach ein $|x|$ verschluckt. Das hätte schon beim Hinschreiben nicht passieren dürfen. Ich glaube außerdem, dass ich mich bei der Berechnung der Varianz vertan habe weil ich stattdessen den Erwartungswert berechnet habe. Echt unnötig. Den Punkt gönne ich mir (6/6)

Takeaways

Ich mache viele Flüchtigkeitsfehler, wie kann ich diese verhindern?

• Bei komischen Antworten unbedingt schauen, was der Fehler ist.
• Meine eigenen Sachen bepunkten, so wie es ein Korrektor machen würde

Berichtigt man die Klausur nach Flüchtigkeitsfehler, bekomme ich insgesamt (43/60) Punkten, also eine 2.0 oder vielleicht noch besser.

Des Weiteren notiere ich mir folgende Sachen:

• Meine Lösung mit offizieller Lösung vergleichen, um Details zu finden
• In Übung wichtige Punkte, auf die man achten muss mitschreiben
• In Übung gehen!
• Bei Themen mit wenig Intuition Literatur oder Tutor aufsuchen