Blätterung

Beschreibung

Eine Blätterung ist im Grund einfach ein Vektorfeld (Vektorraum) ohne Pfeil. Das heißt, dass wir nicht zwischen Vorder und Rückrichtung unterscheiden. Desweiteren ist uns die Länge der Vektoren egal.

Es gibt eine etwas komplizierteres Bild, dass eine Bläterung als Schichten einer Mannigfaltigkeit interpretiert. Die Verschiedenen Schichten bilden eine eigene Mannigfaltigkeit.

Definition

Sei $M$ eine geschlossene Mannigfaltigkeit und sei $X\subseteq M$ eine endliche Menge von Singularitäten. Eine Blätterung $\mathcal{F}$ von $M$ mit Singularitäten $X$ ist eine Zerlegung $\{F_{\alpha }\}$ von $M\backslash X$ in disjunkte wegzusammenhängende Untermengen. Es gibt einen Atlas $({\varphi }_i,U_i)$ von $M$ sodass gilt:

1. Für jeden Punkt $p\in U_i\backslash X$ bildet die Abbildung die Teilmengen $F_{\alpha }$ auf horizontale $k$-Ebenen ${\mathbb{R}}^k\times \{(x_{k+1},...,x_n)\}$ von $R^n$ ab. Kartenübergänge bilden Ebenen auf Ebenen ab.
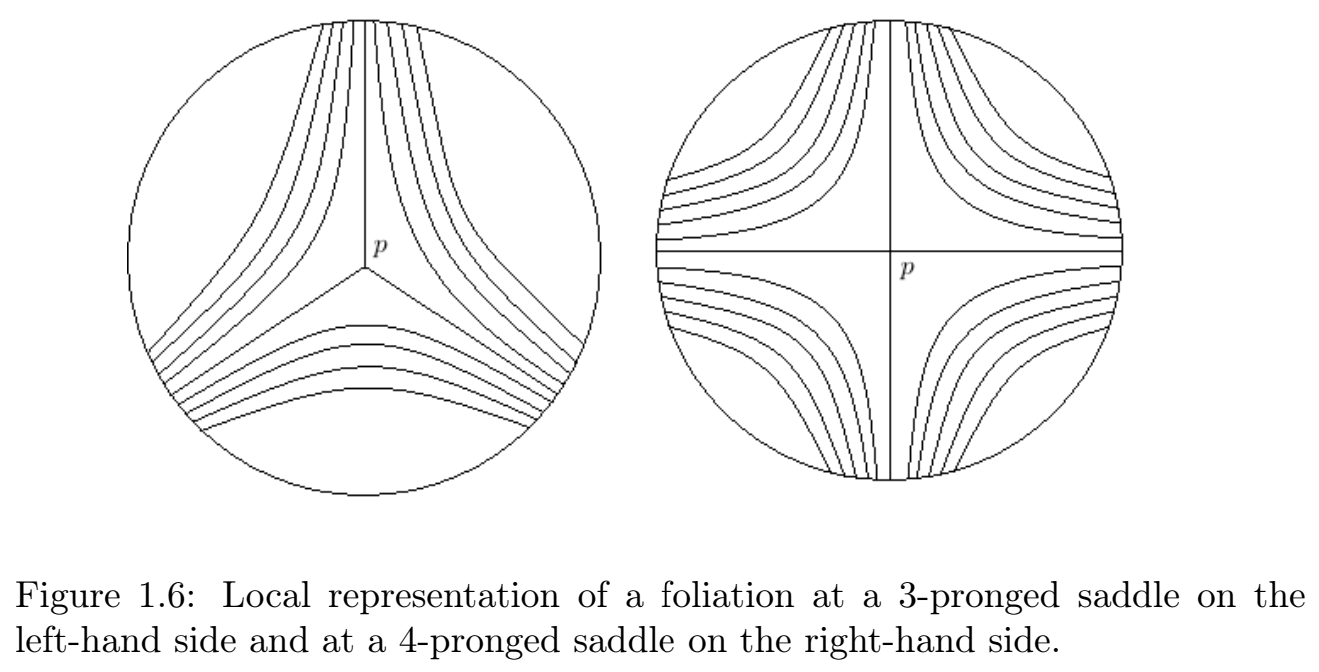
2. Für jeden Punkt $p\in U_i\cap X$ bildet die Karte ${\varphi }_i$ den Punkt $p$ auf einen $k$-zackigen Sattel ab. ($k\ge 3$)

Die Definition “Sieht aus wie ein Sattel” ist ein bisschen komisch aber da wir fast immer an Punkten außerhalb der Singularität arbeiten und da sowieso alles schön aussieht ist das nicht so wichtig.

Ist das betrachtete Objekt eine Mannigfaltigkeit mit Rand oder eine gebohrte, so sind zusätzliche Sachen erlaubt. (Die Regeln sind dabei die gleichen, nach dem wir eine Randkomponente zu einem Punkt zusammenschrumpfen)

Definition (Mannigfaltigkeit mit Rand)

Eine Blätterung darf an einem Punkt konzentrisch sein, eine $1$-zackige Singularität sein oder eine mehr-zackige Singularität sein.

Es ist möglich, eine Blätterung lokal durch eine $1$-Form zu beschreiben. Dies resultiert tatsächlich in eine Verallgemeinerung, bei der Singularitäten mehrunterschiedliche Formen annehmen können.

Charakterisierung durch $1$-Form

Sei $\omega \in {\Omega }^1$ eine $1$-Form um einen Punkt $p\in M$. Lokal, d.h. auf einer Umgebung $p\in U$ ist jede Differentialform exakt, besitzt also eine Funktion $f:U\to M$, sodass $df=\omega$. $f$ hat einen kritischen Punkt g.d.w. $\omega$ verschwindet. An den Stellen definieren wir unsere Singularitäten. Die Blätterung ist definiert als die Levelsets von $f$. (dabei können geschlossene Blätter entstehen. Das ist bei pA-Abbildungen nicht denkbar)

Definition durch $\mathcal{G}$-Gruppe

Es gibt eine Möglichkeit, Blätterungen durch $\mathcal{G}$-Gruppen zu definieren. Schaue dazu in den Artikel der Messbare Blätterung.

Eigenschaften

Euler-Poincaré Formel

Die Euler-Poincaré Formel ist verwandte Version des Hairy Ball Theorem. Sie erstellischen der Anzahl von Singularitäten und der Euler characteristic einer Mannigfaltigkeit. Sei $M$ eine Geschlossene Fläche $2\chi (M)=\sum _{x\in M}2-p(x)$

Kombinatorische Beschreibung

**Blätterucke|Zugstrecken]] beschrct] Passende Blätterung Sine [[Zugeiner Blätterung $\mathcal{F}$, wenn es eine differenierbare Abbildung $f:M\to M$ gibt, die homotop zur Identität ist und $f(M)=\tau$ erfüllt. Außerdem ist das Bild eines Tangentialvektors entlang einer Zugstrecke nie $0$. (d.h. $f$ ist nicht singulär an keinem Punkt der Zugstrecke).

Passende Blätterung

Sine Zugstrecke $\tau$ passt zu einer Blätterung $\mathcal{F}$, wenn es eine differenierbare Abbildung $f:M\to M$ gibt, die homotop zur Identität ist und $f(M)=\tau$ erfüllt. Außerdem ist das Bild eines Tangentialvektors entlang einer Zugstrecke nie $0$. (d.h. $f$ ist nicht singulär an keinem Punkt der Zugstrecke). Die Euler-Poincaré Formel impliziert, dass die $2$-Sphäre keine Blätterung besitzt.

Torus

Die Euler-Poincaré Formel impliziert, dass alle Blätterungen des $2$-Torus regulär sind.

Beispiele

Sphäre