Erklärung zu Gruppen

Gruppen

In der Einführung zur Gruppentheorie kann es passieren, dass man sich hauptsächlich auf zyklische Gruppen fokussiert.

Was sind zyklische Gruppen

Zyklische Gruppen sind nur ein winziger Teilbereich aller Gruppen. Zyklische Gruppen sind meiner Meinung nach auch die speziellsten Gruppen und sind am leichtesten zu verstehen. Zyklische Grupen haben folgende Eigenschaften:

Zyklische Gruppen haben die Struktur einer Uhr

Die Zyklische Gruppe mit 12 Elementen hat mehrere Schreibweisen: $\mathbb{Z}12,C_{12},{\mathbb{Z}}_{12}$ oder $\mathbb{Z}/12\mathbb{Z}$ meine Lieblingsschreibweise ist die zweite, das $C$ steht für cyclic. Wir verwenden im folgenden $\mathbb{Z}12$.

Die Art wie man in $\mathbb{Z}12$ Zahlen addiert und dann kleinere Zahlen erhalten kann funktioniert genauso, wie man zwei Uhrzeiten einer Uhr addieren würde. $5+9=16=4$.

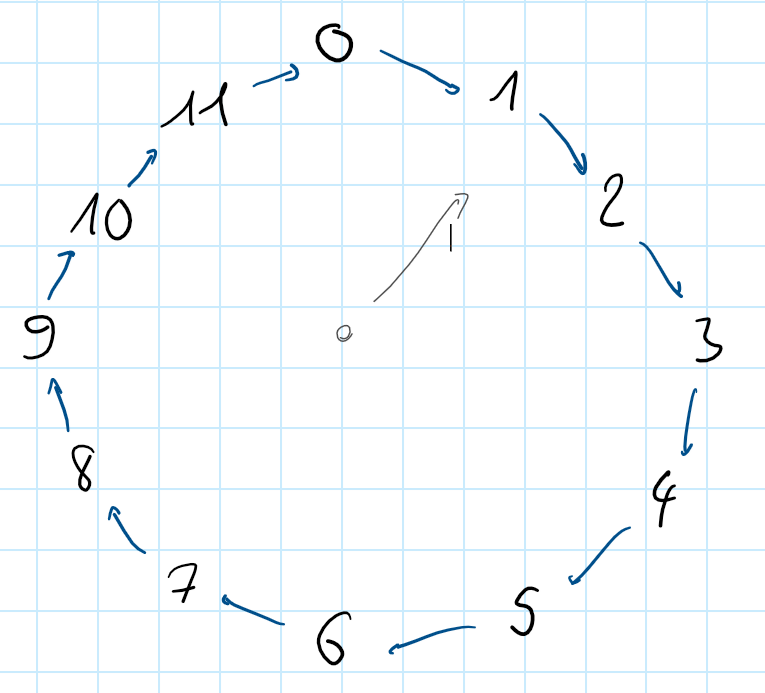
Erzeugendensysteme

Die blauen Pfeile sagen übigens was passiert, wenn man $1$ auf jede Zahl addiert. $0+1=2,7+1=8$. Indem wir einem Pfeil zweimal folgen können wir zweimal die $1$ addieren: $0+1+1=0+2=2$. Wir erkennen, dass man jedes Element von $0$ erreichen kann, wenn man nur genug Pfeilen folgt, das heißt genug $1$ aufaddieren. Diese Eigenschaft, bedeutet, dass die Zyklische Gruppe $\mathbb{Z}12$ von $1$ erzeugt wird (d.h. $\mathbb{Z}12=⟨1⟩$).

Obere Gruppe wird aber nicht nur aus $1$ erzeugt. Die Gruppe wird auch durch $5$ erzeugt, wie man hier erkennen kann: 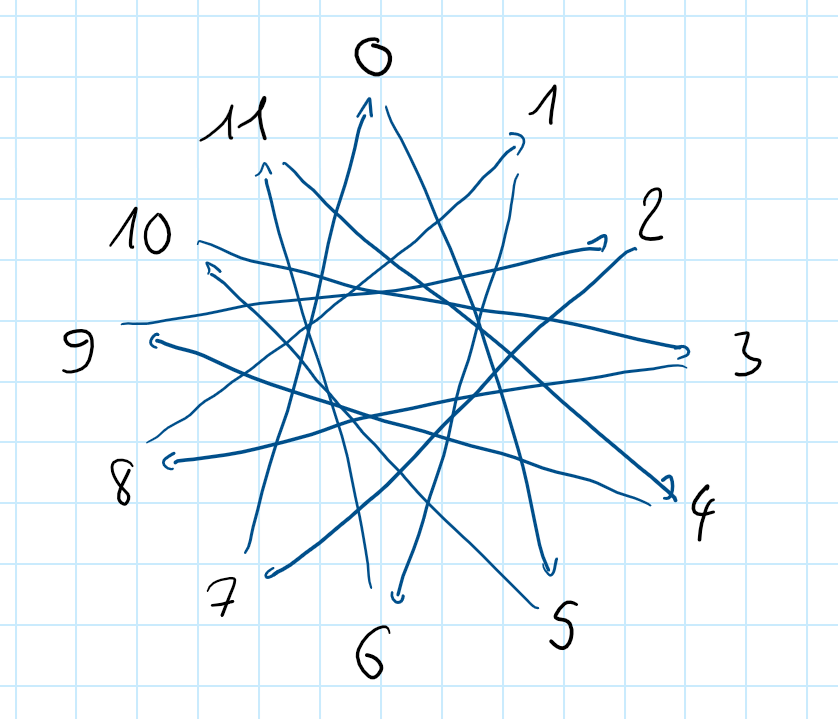Jeder Pfeil repräsentiert das Addieren von $5$ durch genug Aufaddieren von $5$ erreicht man jedes Element. Es gibt also mehrere Möglichkeiten eine Gruppe zu erzeugen! $\mathbb{Z}12=⟨1⟩=⟨5⟩$

Wann wird die Ganze Gruppe $\mathbb{Z}12$ durch ein Element erzeugt? Ich denke, die Aufgabe kann man gut durch ausprobieren lösen. Man findet sehr schnell einen Zusammenhang. Schauen wir, ob $2$ ein Erzeuger ist. 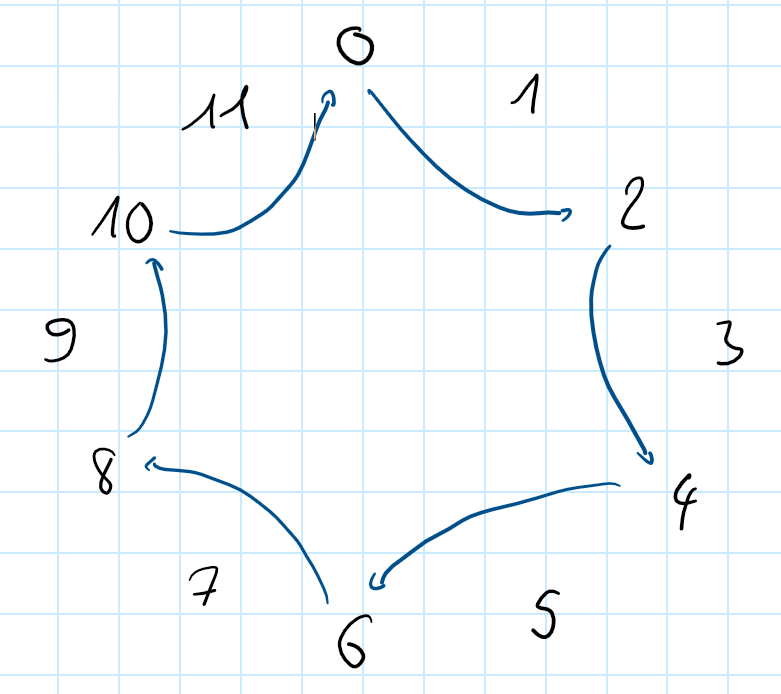Nein, wie man sehen kann, kann man $1$ nicht bekommen, egal wie viele $2$ man zusammenaddiert. Wir erhalten aber stattdessen eine Untergruppe von $\mathbb{Z}12$ mit $6$ Elementen. Die Untergruppe ist auch zyklisch und ist daher strukturgleich zu $\mathbb{Z}6$.

Herausfordernde Aufgabe: $2$ und $3$ sind alleine keine Erzeuger von $\mathbb{Z}12$ Ist die Menge $\{2,3\}$ ein Erzeuger? Welche Eigenschaften müssen für zwei beliebige Zahlen erfült sein, damit sie zusammen ein Erzeuger einer zyklischen Gruppe von Ordnung $n$ sind.

Die verwendeten Diagramme nennt man Cayley-Diagramme und sie sehr äußerst hilfreich zur Visualisierung von Gruppen, Erzeugern und einer Menge anderer Sachen.

Andere Gruppen

Andere Gruppen sind überall. Versuchen wir beispielsweise drei Zahlen vertauschen (permutieren) $1,2,3$. Führen wir eine Vertauschaktion auf die drei Zahlen $1,2,3$ aus, indem wir jede Zahl nach rechts schieben und die ganz rechts nach vorne stellen erhält man die Anordnung $3,1,2$. Jede Vertauschaktion lässt sich durch eine andere Vertauschaktion rückgängig machen. Die obere Vertauschung z.B. machen wir rückgängig, indem wir alle Zahlen wieder nach links schieben $3,1,2\to 1,2,3$. Führt man zwei Vertauschungen hintereinander aus, erhält man eine neue Vertauschung. (z.B. die zweite und dritte Zahl und dann die erste und zweite Zahl zu vertauschen ergibt: $1,2,3\to 1,3,2\to 3,1,2$, was sogar die Vertauschung ist die wir vorhin hatten.) Das Nichtstun ist auch eine Vertauschung.

Damit haben wir alle Anorderungen an eine Gruppe abgearbeitet.

• Die Gruppe ist eine Menge von Vertauschungen
• Die Hintereinanderausführung von Vertauschungen ist eine Vertauschung
• Jede Vertauschung hat eine Inverse Vertauschung
• Es gibt eine Vertauschung, die nichts tut, also neutral ist.

Die Verknüpfung mit der wir zwei Vertauschungen kombinieren ist die Hintereinanderausführung.

Die Gruppe die wir erhalten, wird $S_3$ genannt. Es ist die Gruppe aller Vertauschungen von $3$ Elementen. Müsste man ein Diagramm nach oberem Vorbild zeichnen würde dieses so aussehen:

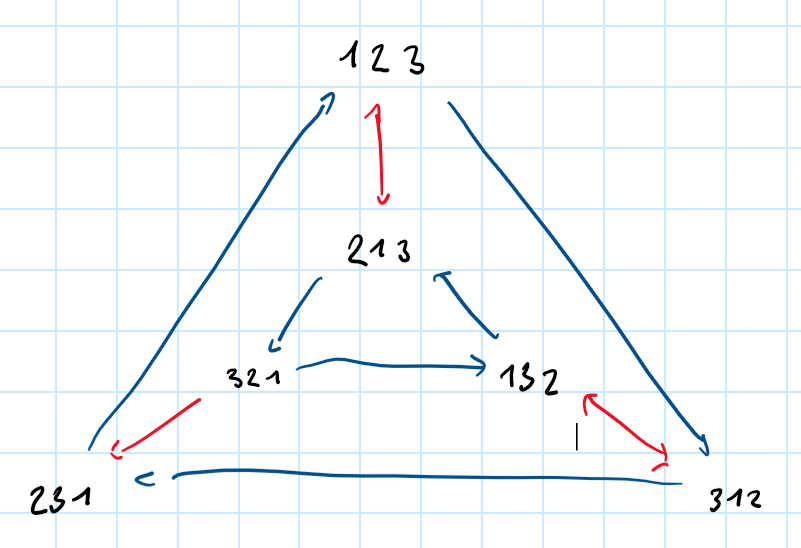Die blauen Pfeile symbolisieren die Bewegung der Ziffern nach rechts. Die roten Pfeile die Vertauschung der zwei ersten Ziffern.

Durch Hintereinanderausführung dieser beiden Vertauschungen kann man alle Vertauschungen von $1,2,3$ erhalten. Die beiden Vertauschungen bilden also ein Erzeugendensystem. Für $S_3$ (und auch für alle anderen Gruppen die nicht zyklisch sind) benötigt man immer mindestens zwei Erzeuger.

Die Ordnung der Untergruppe teilt die Ordnung der Obergruppe

Dass das für zyklische Gruppen gilt habe ich gezeigt, indem ich mit gleichabständigen Lücken argumentiert habe. Gilt das gleiche aber auch für nicht-zyklische Gruppen? Das obere Diagramm zeigt eine nicht-zyklische Gruppe, es sieht jedoch überhaupt nicht aus wie eine Uhr, die gleiche Argumentation können wir nicht anwenden.

Ich habe zwar einen guten Beweis gefunden, ich kann ihn aber nicht auf die obere Gruppe anwenden, da ich dazu mächtigere Formalismen benötige. Ich muss jetzt auch leider weg. Evtl. mache ich aber später weiter.

\newcommand{\R}{\mathbb R}