Leinster - Magnitude homology equivalence of Euclidean sets (Joint work with Adrián Doña Mateo)

Abstract

I will present a theorem describing when two closed subsets X and Y of Euclidean space have the same magnitude homology in the following strong sense: there are distance-decreasing maps X \to Y and Y \to X inducing mutually inverse isomorphisms in positive-degree magnitude homology. The theorem states that this is equivalent to a certain concrete geometric condition. This condition involves the notion of the “inner boundary” of a metric space, which consists of those points adjacent to some other point. The proof of the theorem builds on Kaneta and Yoshinaga’s structure theorem for magnitude homology.

The slides can be found on Tom Leinsters Webpage. https://www.maths.ed.ac.uk/~tl/

How do you type everything so quickly and concise? Do you sometimes have issues prioritizing important stuff? Do you do this outside of the n-category (to remember lectures?). How do you use the notes in the future?

Motivation

Two Homotopic Maps induce the same homology map. Is there an analogous relation between functions that preserve magnitude homology?

Review Homology

We construct a homology of a category

Construction

Take an ordinary category $X$. We can construct a chain complex as follows: $C_n(X)={⨆}_{x_0,...,x_n\in X}\mathbb{Z}\cdot (X(x_0,x_1)\times ...\times X(x_{n-1},x_n))$ Does $X(x,y)$ mean the same as $Hom(x,y)$? There is a differential $\partial =\sum (-1{)}^i{\partial }_i$ where $\partial$ removes the $i$-th term by merging or forgets the first or last factor.

We now generalize to enriched cats (see Roff - Iterated Magnitude homology). The ingredients generalize in the following way:

Magnitude ingredients

A Magnitude is given by

• a monoidal category
• a ring
• A size homomorphism from the cat to the ring

A magnitude homology

• needs a specialized semicartesian monoidal category $V$
• a monoidal abelian category (can multiply) $A$
• a strong symmetric monoidal size functor $\Sigma :(V,\otimes )\to (\mathbb{A},\otimes )$

We want to define a homology for the enriched version too.

Magnitude homology enrichted category

Now define a chain complex as before. Define the differential in the same way. This gives a chain complex which results in a homology theory. The chain complex is $C_n(X)={⨆}_{x_0,...,x_n\in X}\Sigma (X(x_0,x_1)\otimes ...\otimes X(x_{n-1},x_n))$ The magnitude homology is gotten by taking the quotients of the chain complex.

Now we specialize to metric spaces again.

Magnitude homology metric space

For the specialization we need

• monoidal abelian category $A$
• string monoidal functor $\Sigma :[0,\infty [\to A$ Could you explain the terminology?

I skip the concrete definition since it is given in Magnitudenhomologie (Metrischer Raum)! This homology theory is $[0,\infty [$-graded homology theory!

Sample results

• Let $X$ be a closed subset of ${\mathbb{R}}^N$ Then $X\text{ is convex}⟺M{H}_{1,l}(X)=0\text{ for all }l>0$ And if $X$ convex then $M{H}_{n,l}(X)=0$ for all $n\ge 1$ and $l>0$.
• The magnitude homology tells you how big a from ${\mathbb{R}}^n$ cut out hole is (Ryuki Kante &Yoshinaga). e.g. Let $r>0$ and $X=\{x\in {\mathbb{R}}^n:\Vert x\Vert \ge r\}$ Then $r=\sup \{l/2n:M{H}_{n,l}(X)\ne 0\}$

Slogan: The more geodesics are unique the more magnitude homology is trivial!

Preparation Main theorem

What does is mean that two objects have homology?

• Of of the Homology groups are isomorphic (not useful)
• There is a map $X\to Y$ inducing an iso $H_{\ast }(X)\to H_{\ast }(Y)$
• There are two maps between $X$ and $Y$ going in opposite direction, inducing mutually inverse homology maps

Inner boundary of a metric space

Adjacency

Two points are adjacent, if two points are distinct and there is no point in between. The Inner boundary ist the set points which are adjacent to another point. of all adjacent points. $\rho X$

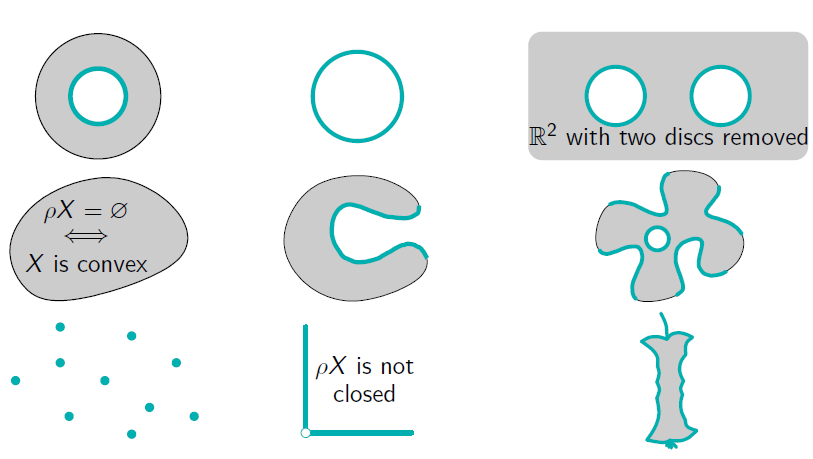We are using the metric of the ambient space!

Closure of the inner boundary and hull

$\overline{\text{conv}(\rho X)}$ is the closure of the inner boundary. The $core(X)$ is the intersection of the hull with the Set.

Main Theorem (Leinster & Mateo)

Take two sets of ${\mathbb{R}}^n$. Then two spaces are magnitude homologic, if

• there are distance-decreasing maps $X\rightleftarrows Y$ inducing mutually inverse magnitude homology maps for all $n\ge 1$
• there are distance-decreasing maps $X\rightleftarrows Y$ inducing mutually inverse magnitude homology maps for some $n\ge 1$
• The $core(X)$ and $core(Y)$ are isometric.

The Proof

The ingredients:

• Kante and Yoshinagas structure theorem for magnitude homology
• An analysis of when two maps $X\rightrightarrows Y$ of metric spaces induce the same map in magnitude homology
• Some convex geometry

I’ll skip over the rest as I dont think it is very important.

Straight metric spaces

Definition straight metric spaces

$[x,y]$ is the set of all points, which sit between $x,y$. Call $X$ as a space straight, if any points in sa suitable order devide the space.

i.e. the betweenness relation behaves as in subsets of ${\mathbb{R}}^N$.

Kaneta and Yoshinagas structure theorem

An Element of $M{H}_{n,\ast }(X)$ is an equivalence class of cycles $x=(x_0,...,x_n)$.

Thinness

An $(n+1)$-Tuple of points $x=(x_0,...,x_n)$ ist thin if.

• $x_{i-1}$ and $x_i$ are adjacent for all $i$.
• $x_i$ is not between $x_{i-1}$ and $x_{x^1}$ for any $i$.

Then every $x_i$ is in $\rho X$ and $x$ is automotaically a cycle.

Points like be above will not be found in graphs but can be found on the border of closed euclidian sets.

Theorem

If $X$ is straight then $M{H}_{n,\ast }(X)$ ist freely generated by the set of thin $(n+1)$-tuples

A corollary of the above is the following:

Corollary

Let $X$ be a straight metric space. Then any retract of $X$ containing its inner boundary has the same homology as $X$.

When are two maps the same in homology?

Theorem

Take maps of metric spaces $X\rightrightarrows Y$ with $X$ straight. If $f{|}_{\rho X}=g{|}_{\rho X}$, then $C_{\ast ,\ast }(X)\rightrightarrows C_{\ast ,\ast }(Y)$ are chain homotopic in degree $\ge 1$ and therefore the induced maps are equal.

When does a self-map induce the identity in homology

Theorem

Let $X$ be a straight metric space. The following conditions on a self-map $e:X\to X$ are equivalent.

• $e_{\ast }:M{H}_{n,\ast }(X)\to M{H}_{n,\ast }(X)$ is the identity for all $n\ge 1$
• $e_{\ast }:M{H}_{n,\ast }(X)\to M{H}_{n,\ast }(X)$ is the identity for some $n\ge 1$
• $e$ is the identity on the inner boundary of $X$