Alexander-Polynom

8

Beschreibung

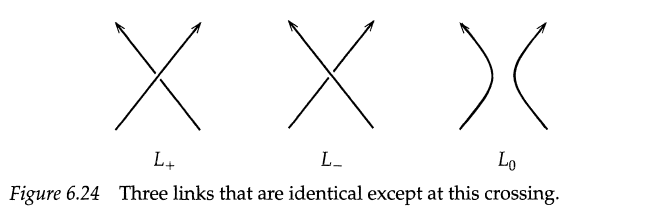
Das Alexander-Polynom ist eine Invariante eines Knoten. Das Alexanderpolynom berechnet sich durch Rekursion. Effektiv nehmen wir einen Knoten und verändern eine Kreuzung auf zwei verschiedene Arten, sodass zwei einfachere Knoten herauskommen. Das Polynom errechnet sich aus der Summe der beiden einfacheren Polynome.

Ich werde erstmal keine exaktere Definition angeben, da dies für meine Zwecke nicht ganz so wichtig ist.

Definition:

Das Alexander-Polynom berechnet sich aus zwei Regeln.

1. Der triviale Knoten hat das Polynom $1$
2. Es gilt die Skein-Relation, das Verändern einer Kreuzung verändert das Polynom auf folgende Weise: $\Delta (L_{+})-\Delta (L_{-})+\left(t^{\frac{1}{2}}-t^{-\frac{1}{2}}\right)\Delta (L_0)=0$

Eigenschaften

Satz: Symmetrie

Das Alexander-Polynom ist symmetrisch unter ${\Delta }_K(t)={\Delta }_K(t^{-1})$

Vermutung: Trapezoidalvermutung

Fox stellte die Vermutung auf, dass für Alternierender Knoten die Koeffizienten des Alexander-Polynoms Trapezoidal sind: Sie steigen erst, bleiben dann flach und fallen dann wieder ab.

Beispiele

Beispiel: Kleeblattschlinge

Die Kleeblattschlinge hat das Polynom $\Delta (t)={\left(t^{\frac{1}{2}}+t^{-\frac{1}{2}}\right)}^2+1=t-1+t^{-1}$

Beispiel: Achterknoten

Das Polynom des Achterknoten ist $\Delta (t)=-t+3-t^{-1}$

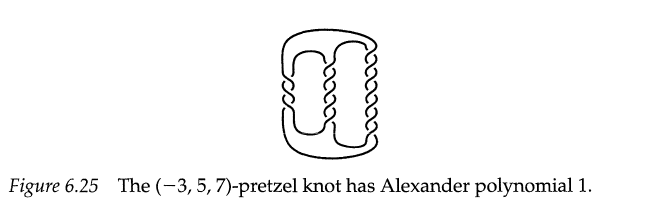
Beispiel: Nicht-Trivialer Knoten mit Polynom $1$

Die $-3,5,7$-Brezelverschlingung hat Alexanderpolynom $1$: