Diedergruppe

Beschreibung

Eine Diedergruppe beschreibt die Rotations- und Achsensymmetrien eines regelmäßigen Polygons

Diedergruppen eines $n$-Ecks werden mit $D_n$ bezeichnet.

Aussehen

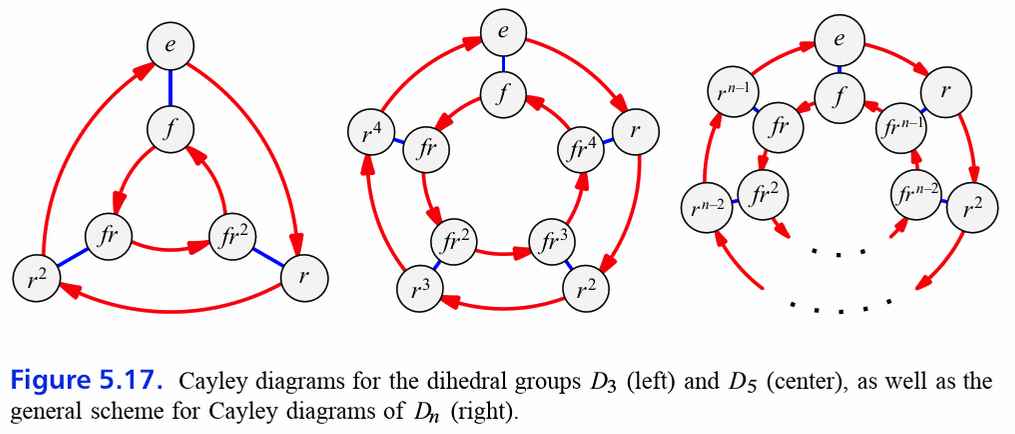
Cayley-Diagramm

Multiplikationstafel

*Beobachte, dass die Tafel aussieht, als bestünden die Quadranten aus vier Multiplikationstafel von zyklischen Gruppen. *

Zykelgraph

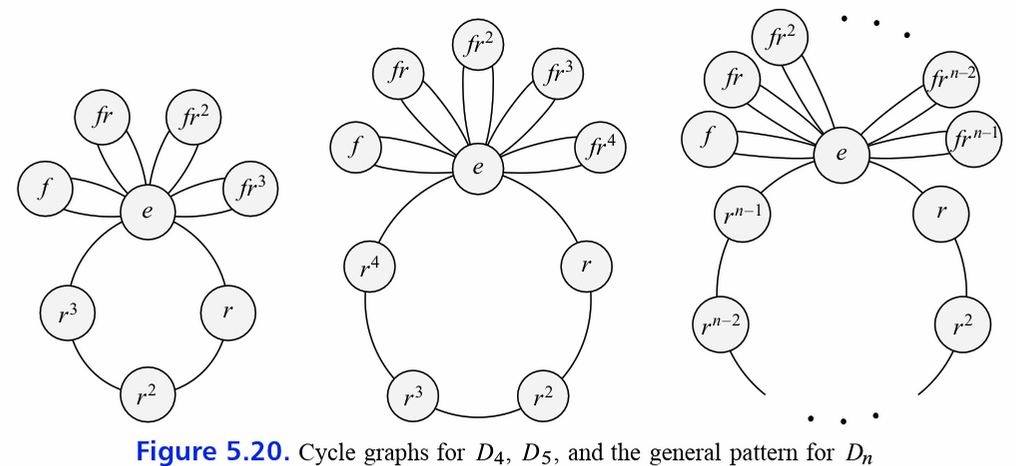Der Zykelgraph einer Diedergruppe besteht immer aus einem großen Ring der Größe $n$ und $n$ kleinen Ringen der Größe $2$

Definition

Untergruppe von $S_n$

Sei $n\in \mathbb{N}$ mit $n\subseteq 3$. Dann wird die Untergruppe $D_n=⟨{\sigma }_n,{\tau }_n⟩$ von $S_n$ die $n$-te Diedergruppe genannt.

$\sigma$ ist der $n$-Zykel

Präsentation

Die Diedergruppe hat die Präsentation $D_n\cong \text{wink}\text{ges}r,s\mid \text{ges}{s}^2,r^n,srsr$

Charakterisierungen

Semidirketes Produkt

Für alle $n\in \mathbb{N}$ mit $n\subseteq 3$ gilt $D_n\cong \mathbb{Z}/n\mathbb{Z}{⋊}_{\varphi }\mathbb{Z}/2\mathbb{Z}$. Insbesondere ist $D_n$ eine nicht-abelsche Gruppe der Ordnung (Gruppe) $2n$.

Eigenschaften

Zusammenhang zu zyklischen Gruppen

$D_n$ hat doppelt so viele Elemente wie die Zyklische Gruppe $C_n$

Semidirektes Produkt

Sei $n\in \mathbb{N}$ mit $n\ge 3$ eine Gruppe und $\{g,h\}$ ein Erzeugendensystem von $G$, wobei $ord(g)=n,ord(h)=2$ und $ghgh=e_G$ gilt.

Sei außerdem ein Gruppenhomomorphismus definiert: ${\varphi }_n:\mathbb{Z}/2\mathbb{Z}\to Aut(\mathbb{Z}/n\mathbb{Z})$ gegeben durch $\varphi (\bar{0})=id$ und $\varphi (\bar{1})=(gN)$ bla bla bla

Auf jeden Fall ist $G$ isomorph zum Semidirekten Produktkturen/3. Gruppentheorie/Elementare Gruppentheorie/2. Erzeugung von Gruppen/Produkte und Quotienten/Semidirektes Produkt/Semidirektes Produkt/Semidirektes Produkt|Semidirekten Produkt]] $\mathbb{Z}/n\mathbb{Z}{⋊}_{{\varphi }_n}\mathbb{Z}/2\mathbb{Z}$¹

Und das ist genau Semidirektes ProduktBeispiele

Die Gruppe $D_2$

$D_2$ ist einfach die Klein 4-Gruppe_Bild_1

Die Gruppe $D_3$

Wie man im Artikel über Neuverkabelung lesen kann, ist $D_3$ ein Semidirektes Produkt von $C_2$ und $C_3$:

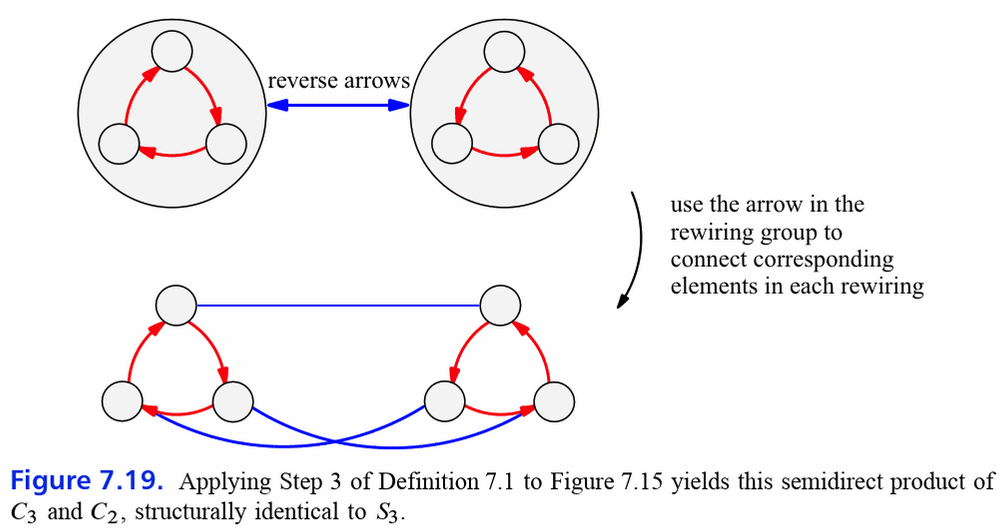
lit_carterVisualGroupTheory2021

Footnotes

1. Gerkmann - Proposition 7.6 ↩