Bestvina-Handel-Algorithmus

Beschreibung

Der Bestvina-Handel-Algorithmus generiert eine Invariante Zugstrecke für einen gegebenen Pseudo-Anosovscher Homöomorphismus, beschrieben durch Dehn-Twists. Die grundlegende Idee ist, mit einer simplen Zugstrecke zu beginnen, und diese anzupassen, bis die “effizienteste” Zugstrecke herauskommt.

Verhalten für Zöpfe

Sei $\beta$ ein Zopf, welcher eine Klasse von Homöomorphismen der Kreisscheibe symbolisiert. Wir beginnen mit einer starken Vereinfachung der Zugstrecke, dem sogenannten Liniendiagramm. Hierbei werden die Knoten der Reihe nach durch Strecken verbunden. Wir erweitern dann das Diagramm um periphere Zweige. Wir tun dies auf eine Weise, dass auch nach dem Herumwickeln das Diagramm auf die ursprüngliche Strecke gequetscht werden kann. Wenn die Zugstrecke dann bereits invariant ist, haben wir Glück gehabt und wir sind fertig. Das ist bei besonders einfachen Zöpfen üblicherweise der Fall. Sonst muss man die Zugstrecke verändern. Siehe dazu Thiffeault

Definition: Allgemeiner Bestvina Handel

Sei $S$ eine Fläche mit mindestens einer Bohrung. Bevor wir Zugstrecken betrachten, betrachten wir Graphen. Wir fangen hierbei mit einem einfachen Graphen an und machen diesen Schrittweise effizienter. Eine natürliche Wahl für den ersten Graphen ist dessen Rückgrat. Wir untersuchen nun einen Homöomorphismus $f:S\to S$. Das Bild von $G$ unter $f$ kann durch eine Isotopie auf eine Gefaserte Fläche von $G$ verschoben werden (Indem wir die gleiche Retraktionsdeformation wir beim Rückgrat verwenden). Eine weitere Isotopie macht daraus eine Abbildung, die eine Graphabbildung induziert. Wir bezeichnen diese als $g$. Dies ist besonders simpel, wenn $f$ durch Dehn Twists um Kurven beschreibbar ist und wir unser Rückgrat so wählen, dass die Kurven darin liegen. Der Algorithmus läuft in folgenden Schritten ab:

1. Falls $g(G)$ Pfade Rückwärts läuft, können wir $f$ durch eine Isotopie so anpassen, dass keine Rückwärtsbewegungen mehr vorhanden sind

2. Falls $g$ einen invarianten nicht-trivialen Wald besitzt (d.h. ein Teilgraph in Form eines Baumes der unter $g$ auf sich selbst abbildet), wenden wir eine Isotopie an, um den Baum auf eine Polygonkomponente zusammenzuziehen. Wenn nötig gehe zu 1 zurück

3. Wenn $G$ Knoten von Valenz $1$ hat, können wir diese in den benachbarten Knoten verschmelzen. Wenn nötig gehe zu 1 und 2 zurück

4. Enthält $G$ einen nicht-trivialen invarianten Teilgraph, so ist $f$ isotop zu einem Reduzibler Homöomorphismus. Wegen Schritt 2 gibt es keine invarianten Bäume, und der nicht-triviale invariante Teilgraph besitzt damit einen Zykel. Dieser Zykel wird wegen irgendeiner Annahme nicht auf einen Punkt abgebildet und ich nicht auf eine Strecke, (da der Graph sonst rückwärts laufen müsste). Somit wird der Zykel auf einen anderen Zykel im Teilgraph abgebildet. Es lässt sich dann eine Menge von Zykeln im Teilgraph finden, die sich untereinander permutieren.

5. Ab diesem Schritt ist bekannt, dass $f$ irreduzibel ist. Wenn es Valenz $2$ Knoten gibt können wir diese mit einem der beiden Nachbarn verschmelzen. Falls nötig, gehe zurück zu 1 oder 4

6. Wenn die Abbildung effizient ist hält der Algorithmus. Sonst existiert ein $k\in \mathbb{N}$ und ein Punkt $p$ im Inneren einer Kante $e$, sodass $g^k$ nicht lokal injektiv ist. D.h. $p$ wird unter $g^k$ auf einen Knoten abgebildet, der die Spitze einer Rückwärtsbewegung ist. Wir wählen unser $k$ minimal. Dann ist $v_1=g(p)$ ein Knoten. Wenn nicht, dann könnte man $g(p)$ als Punkt im Inneren einer Kante wählen, der unter Anwendung von $g^{k-1}$ auf einen Knoten abgebildet wird der Spitze einer Rückwärtsbewegung ist. (Widerspruch zur Minimalität) Wir können die Kante $e$ aufteilen, indem wir $p$ zu einem neuen Knoten machen. Die Idee ist nun die Kanten an $v_{k-1}=g^{k-1}(p)$ zu verschmelzen, damit die neue Kante eine Rückwärtsbewegung enthält. Wir wiederholen das für $g_{k-2}(p)$, u.s.w. bis wir die Kanten bei $p$ Verschmelzen und die Rückwärtsbewegung durch eine Isotopie entfernen können. Es gibt einige Details, die man beachten muss. Mehr Infos in Issas Arbeit.

Haben wir eine effiziente Graphabbildung gegeben, können wir dessen Dilatation als größten Eigenwert dessen Inzidenzmatrix (Zugstrecke) berechnen. Ist der Wert $1$, dann ist die Abbildung periodisch.

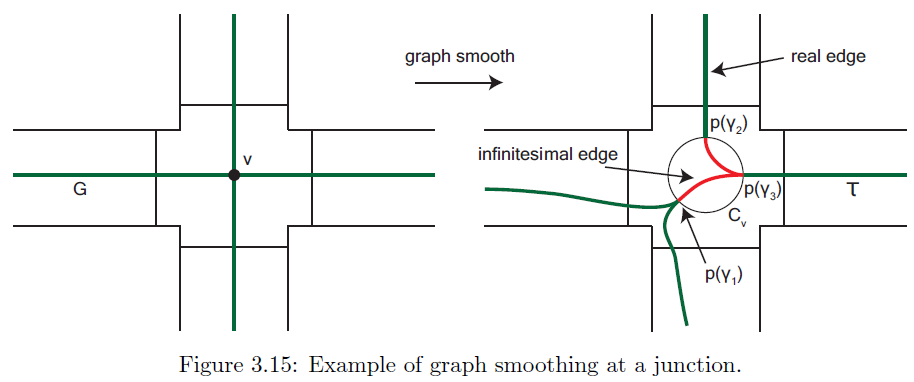
Um nun aus dem Graphen eine Zugstrecke zu machen, nutzen wir die dynamischen Eigenschaften der Zugstrecke aus. Wir erinnern uns, dass ein Tor einer Graphabbildung eine Äquivalenzrelation von benachbarten Kanten (benachbart, da die Abbildung von einem Homöo induziert ist). Diese Kanten werden unter einer Potenz von $g$ auf eine gemeinsame Startkante abgebildet. Demnach wollen wir, dass all diese Kanten in eine Kante zusammenfließen. Jetzt müssen wir nur noch die Tore innerhalb eines Knotens verknüpfen. Dies machen wir folgndermaßen: Wir zeichnen eine Kurve zwischen zwei Toren ${\gamma }_1,{\gamma }_2$, wenn irgendeine Kante des Graphen durch eine Potenz von $g$ auf einen Pfad abgebildet wird, der durch ${\gamma }_1$ reingeht und durch ${\gamma }_2$ rausgeht.

Es kann passieren, dass nach dem Zeichnen der Graphen $\tau$ nicht mehr die Fläche füllt, d.h. nicht jede Komponente ist homöomorph zu einer (einfach punktierten) Kreisscheibe. In dem Fall kann man eine essentielle Kurve finden, die bis auf Isotope unter $f$ erhalten bleibt und $f$ ist isotop zu einem Reduzibler Homöomorphismus.

Die roten Zweige im oberen Bild nennen wir infinitesimale Zweige (die sich ähnlich zu peripheren Zweigen verhalten) alle anderen werden als echte Zweige bezeichnet. Innerhalb eines Knotens kann die Zugstrecke folgende Formen annehmen:

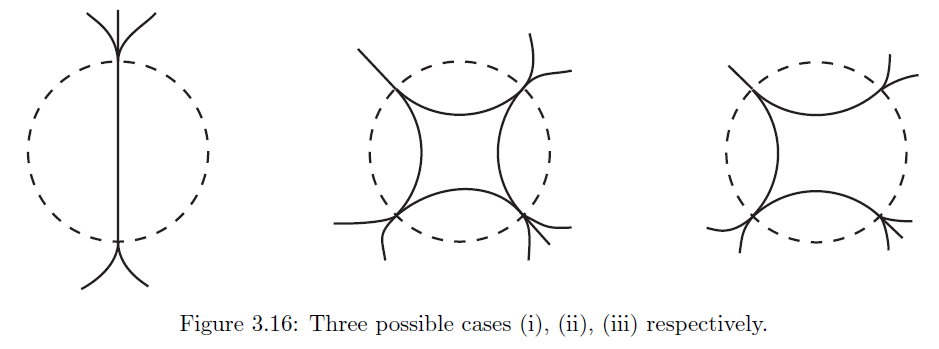
1. Ein ununerbrochener Zwei
2. Ein Polygon
3. Ein Polygon, dem eine Seite fehlt

Eigenschaften

Eigenschaft

iffeaultBraidsDynamics2022]] lit_issa2012construction