Beschreibung
Was sind die Symmetrien eines beliebigen Polytops? Ein Polytop ist die Verallgemeinerung eines Polygons in höheren Dimensionen.
Definition
Eigenschaften
Beispiele
Rotationssymmetrien eines Würfels
Durch Nachdenken finden wir folgende Aktionen:
- Identität
- Rotationen um eine Koordinatenachse
- Rotationen um eine Diagonale durch zwei Gegenüberligende Seiten
- Roationen um die Mittelpunkte gegenüberligender Kanten
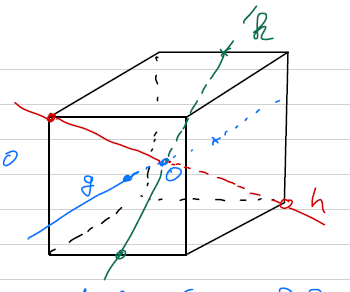
Damit erhalten wir insgesamt verschiedene Aktionen.
Jede Isometrie muss Geraden auf Geraden abbilden, d.h. Diagonalen zwischen gegenüberliegenden Punkten müssen auf gegenüberliegende Diagonalen abbilden. Die Isometrien des Würfels müssen damit ein Teil der Permutationsgruppe aller Diagonalen sein. Da die Permutationsgruppe aber bereits Elemente besitzt, müssen die Rotationssymmetrien eines Würfels isommorph zu sein.