Komplexe Logarithmusfunktion

Beschreibung

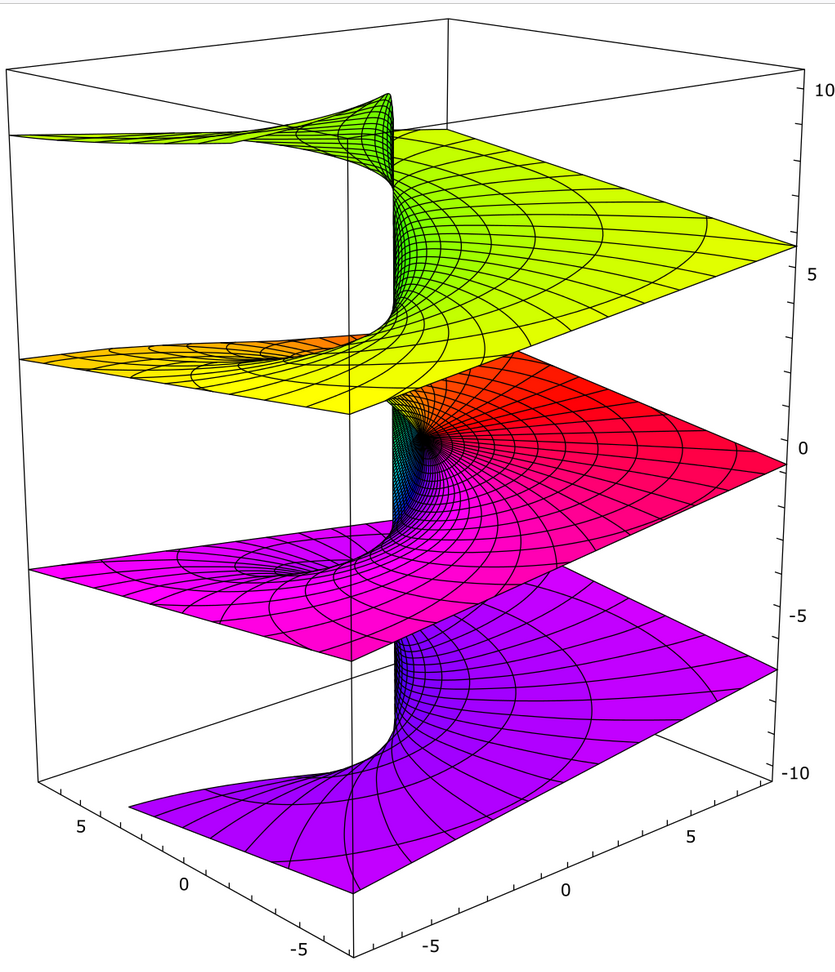
Der komplexe Logarithmus ist die Umkehrabbildung der komplexen Exponentialfunktion. Diese Definition bringt aber einige Probleme mit sich: So ist zum Beispiel das Urbild der Punktmenge $\{e\}$: ${\exp }^{-1}(\{e\})=\{e+2\pi i:k\in \mathbb{Z}\}$ Die Umkehrfunktion von $e^z$ ist also offensichtlich nicht eindeutig.[^1] Die Umkehrfunktion ist aber trotzdem stetig. Was passiert, ist dass die Umkehrfunktion eine Schraube bildet, die sich immer weiter nach unten windet.

Definition

Zweig des Logarithmus

Sei $\varnothing \ne U\subseteq \mathbb{C}\backslash \{0\}$ ein Gebiet. Eine stetige Funktion $\log :U\to \mathbb{C}$ heißt ein Zweig des Logarithmus auf $U$, wenn $e^{\log (z)}=z$ für alle $z\in U$ gilt.¹ Die Bedingung sieht aus, als wäre log eine Umkehrfunktion, das ist sie aber nicht.

In dem Fall ist $\log$ analytisch

Hauptzweig des Logarithmus

Auf $\mathbb{C}\backslash ]-\infty ,0]$ existiert ein Zweig des Logarithmus, der für reelle Werte genau der natürliche Logarithmus ist. $Log(z):=\underset{[[[1,z]]]}{\int }\frac{1}{\xi }d\xi$²

Äquivalente Definitionen

Potenzreihe

Der Hauptzweig des Logarithmus hat die Potenzreihenentwicklung: $\ln (z+1)={\sum }_{n=1}^{\infty }(-1{)}^{k+1}\frac{z^k}{k}=z-\frac{z^2}{2}+\frac{z^3}{3}-...$ Das erhält man, indem man $\frac{1}{z+1}$ als Potenzreihe ausschreibt und integriert.

Eigenschaften

Ableitung

Die Ableitung für jeden Zweig des Logarithmus ist $lo{g}^{\prime }(z)=\frac{1}{z}$ für alle $z\in U$³

Stammfunktion von 1/x

Sei $\varnothing \ne U\subseteq \mathbb{C}\backslash \{0\}$ ein Gebiet. Dann sind äquivalent:

1. Es existiert ein Zweig $log:U\to \mathbb{C}$ des Logarithmus auf $U$
2. $f:\begin{array}{rcl}U& \to & \mathbb{C}\\ z& \mapsto & \frac{1}{z}\end{array}$ besitzt auf U eine analytische Stammfunktion.
3. Für jede Komplexe Stückweise Differenzierbare Schleife $\gamma :[0,1]\to U$ in $U$ ist $n(\gamma ,0)=0$⁴

Das ist ziemlich offensichtlich. Zum einen ist der log die Stammfunktion von $\frac{1}{z}$, also ist es irgendwie klar, dass $\frac{1}{z}$ eine Stamfunktion besitzt. Zum anderen muss $\log$ stetig sein. Und das geht aufgrund der Schraubenform nur dann, wenn man in $U$ keine Schleife um $0$ legen kann. (Also $U$ einfach zusammenhängend ist) Aber dann ist jedes Wegintegral um eine Schleife gleich $0$.

Differenz zweier Zweige

Sei

• $\varnothing \ne U\subseteq \mathbb{C}\backslash \{0\}$ ein Gebiet.
• $f,g:U\to \mathbb{C}$ Zweige des Logarithmus.

Dann ist $f-g$ eine konstante Funktion, die nur die Werte $2\pi i\mathbb{Z}$ annehmen kann.⁵

]: https://www.youtube.com/watch?v=SYxyemNSSm8

Footnotes

1. Zenk - Definition 23.3.1 ↩

2. Zenk - Bemerkung 23.3.4 ↩

3. Zenk - Lemma 23.3.2 ↩

4. Zenk - Satz 23.3.3 ↩

5. Zenk - Lemma 23.2.5 ↩