Uniform convergence

Description

Eine Funktionenfolge heißt gleichmäßig konvergent, wenn die Geschwindigkeit mit der die Funktion punktweise gegen einen Grenzwert konvergiert nicht vom Funktionswert abhängt. Man stellt sich vor, dass der Epsilon-Schlauch um die Zielfunktion gleichmäßig enger wird.

Der Begriff wurde eingeführt als eine stärkere Form der Konvergenz, die es erlaubt, wichtige Eigenschaften wie Stetigkeit oder Integralbildung auf die Grenzfunktion zu übertragen.

Definition

Die Folge $(f_n{)}_{n\in \mathbb{N}}$ konvergiert genau dann gleichmäßg gegen $f$, wenn $\underset{n\to \infty }{\lim }\sup x\in D_f|f_n(x)-f(x)|=0$ Das ist genau dann gegeben, wenn $\forall \epsilon >0:\exists N\in \mathbb{N}:\forall n\ge N:|f_n(x)-f(x)|<\epsilon$

Properties

Exchangable under integral

For uniform convergence the limit and the integral can be exchanged ${\lim }_{n\to \infty }{\int }_a^b{f}_n(x)dx={\int }_a^b{\lim }_{n\to \infty }{f}_n(x)dx={\int }_a^{b}f(x)dx$

Preserves continuity

If the $f_n$ are continuous, then $f$ is continuous too.

Example

Punktweise aber keine gleichmäßge Konvergenz

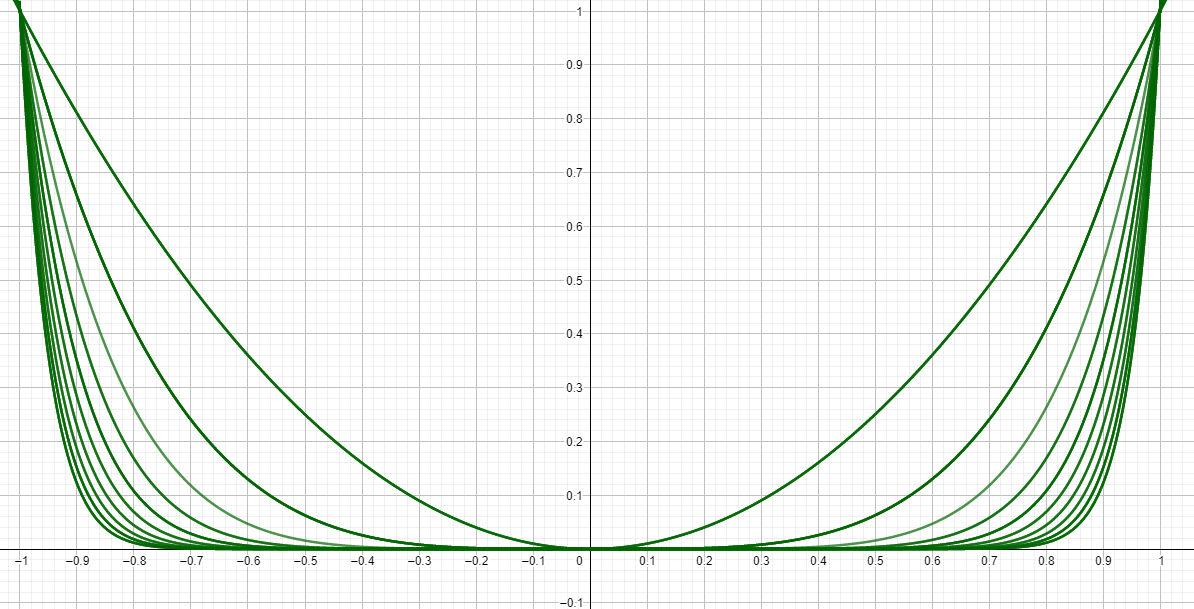Die Funktionenfolge $x\mapsto x^{2n}$ konvergiert punktweise gegen eine Funktion, die überall $0$ ist außer bei $\pm 1$, wo sie $1$ ist. Das Supremum oben konvergiert nicht gleichmäßig gegen $0$. Da es in einer Umgebung um $x_0=1$ immer ein $x$ gibt, bei dem $f_n(x)\approx 1$.