Beschreibung
Im folgenden Artikel werden die Agol Zykel der dreifach punktierten Kreisscheibe betrachtet. Die Idee ist hier im Wesentlichen die Zugstrecke des durchbohrten Torus auf die Kreisscheibe zu reduzieren.
Definition
Betrachte den Torus unter der Hyperelliptische Involution. Diese hat Fixpunkte, die wir als markierte Punkte verstehen können. Bildet man den Quotientenraum und entfernt die Fixpunkte erhält man die -punktierte Sphäre , realisiert als ein Kissen, dessen Ecken fehlen. Durch Aufblasen einer Ecke erhalten die die -Punktierte Kreisscheibe. Die Mapping class group der -Punktierten Sphäre geht analog aus dem Quotienten mit der Hyperbolischen Involution hervor. Fixiert man den vierten Punkt, ergibt sich die Abbildungsklassengruppe der -Braid, die den Rand mengenweise fix hält. Es handelt sich hier also um eine Teilmenge der MCG der -punktierten Sphäre. Die Abbildungsklassengruppe, die den Rand punktweise fix hält lässt sich dann ebenfalls einfach daraus rekonstruieren. Wir erhalten dadurch den folgenden Homomorphismus Sei nun ein Zopf und die zugehörige Wirkung auf dem Kissen. Die Wirkung besitzt eine Geodätische Laminierung und die folgende Zugstrecke ist passend dazu:
Es gibt ein Verhältnis , sodass das wiederholte Anwenden maximalen Spaltungen eine Folge von Links-, und Rechtsspaltungen beider großen Zweige ist. Die Folge von Links- und Rechtspaltungen ist genau durch gegeben. Die Zykellänge ist .
Eigenschaften
Korollar: Konjugatonsproblem für Zöpfe
Ein Korollar der oberen Berechnung ist, dass zwei pseudo-Anosovschen Zöpfe genau dann konjugiert in sind, wenn ihre Agol-Zykel äquivalent sind.
Satz: Zykellänge
Die Zykellänge ist gleich der kanonischen Länge der Linksnormalform.
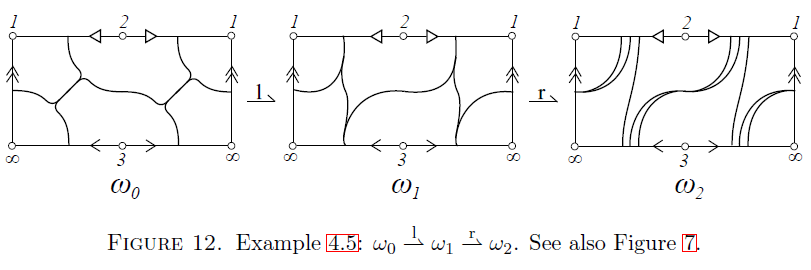
Beispiele
Beispiel:
Sei und . Dann bildet einen Agol Zykel von Länge .