Differentiable function

Description

A function is called differentiable if the slope is defined and continuous everywhere.

Definition

Let $U\subseteq \mathbb{R}$ and $f:U\to \mathbb{R}$. $f$ is differentiable in $a\in U$ if the limit ${\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}=:f^{\prime }(a)$ exists. The limit is denoted by $f^{\prime }(a)$. $f$ is called differentiable if it is differentiable in every point.

Properties

Tip

Examples

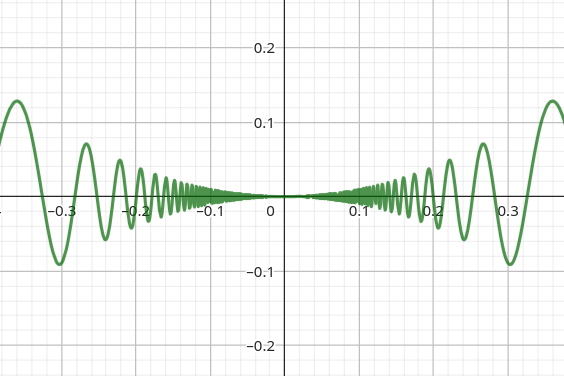
A differentiable function whose differential is not continuous

The function $f:[0,1]\to \mathbb{R},x\mapsto x^2\sin (\frac{1}{x^2}),0\mapsto 0$ has a well defined differential everywhere. Do to the parabolic decrease the differential in $0$ is $0$ but in the neighbourhood it is unbounded.