Greens Satz

Beschreibung

Greens Satz ist der Schwestersatz vom Divergenzsatz. Statt der Divergenz (Lineare Algebra) wird hier jedoch der Rotor (Lineare Algebra) über eine kompakte Menge integriert.

Definition

Sei $K$ ein (vermutlich kompakter) Raum und $X:K\to V^n$ in Vektorfeld (Vektorraum). Dann gilt ${\int }_K\nabla \times XdA={\int }_{\partial K}t\cdot Xdl$ $n$ ist hier die Tangente zum Rand von $K$.

Beweis: Der Rotor beschreibt, wie sich das Wasser an einem Punkt dreht. Warum die Drehung des Wassers hier gleich der Drehung am Rand von $K$ ist ist etwas schwieriger zu begreifen aber das Bild sollte es hoffendlich klar machen:

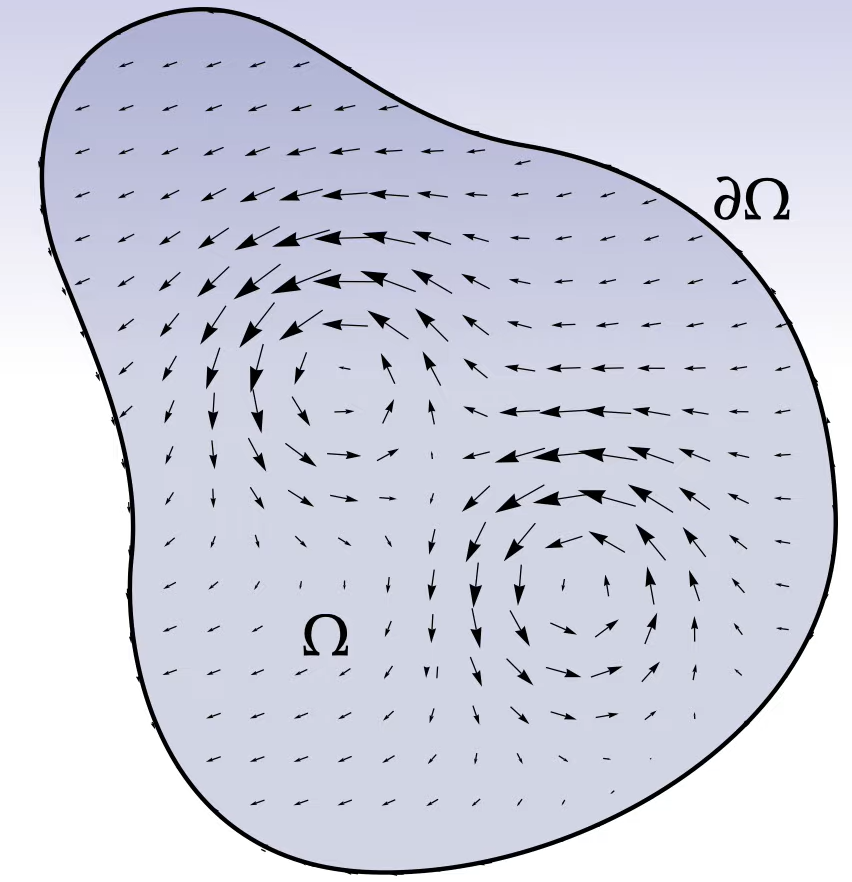
Definition durch das Äußere Differential

Greens Satz kann durch ein Äußeres Differential beschrieben werden. Verwende statt einem Vektorfeld eine $1$-Differentialform $\omega$. Man erhält: ${\int }_{K}d\omega ={\int }_K\omega$ Die Darstellung sieht sehr ähnlich wie Stokes Satz aus!

Eigenschaften