Beschreibung
Wie können die Schritte der Graßmann-Algebra für Dualisierte Vektorräume wiederholen. Dadurch erhalten wir interessante Zusammenhänge zur Multilineare Abbildung.
Man erhält am Ende dadurch spezielle -Formen, mit denen wir -Vektoren aus der Kovariante Tensoralgebra messen können.
Definition
Die Duale Graßmann-Algebra ist definiert durch: und analog
Die Schreibweise mit dem oben oder unten wird von Herr Hensel und Wikipedia nicht immer eingehalten. Das ist mit Vorsicht zu genießen.
Eigenschaften
Identifikation mit Alternierenden Multilinearen Abbildungen
Da die Kontravariante Tensoralgebra mit Multilineare Form ientifiziert werden kann und einfach alle Tensoren enthält, die keine zwei gleichen Werte erhält, kann man, mit Alternierende Form identifizieren.
Natürliches Produkt für Multilineare Alternierende Formen
Durch das Keilprodukt erhält man eine natürliche Operation, um Formen zu multiplizieren. Auf multilinearen alternierenden Formen gibt es ein Produkt \begin{align}(\omega \land \eta): V^{r+s} &\to \R \\ (v_1, ..., v_{r+s}) &\mapsto \frac{1}{r!s!} \sum_{\sigma \in \sum_{r+s}} sgn(\sigma) \omega(v_{\sigma(1)}, ..., v_{\sigma(r)})\eta(v_{\sigma(1)}, ..., v_{\sigma(s)}) = \frac{(r+s)!}{r!s!}A(w \otimes \eta)\end{align} Gemeint sind alle alle Permutationen
Umschreibung des Produktes
Das Produkt alternierenden Abbildungen induziert durch das Keilprodukt lässt sich berechnen durch:
Für mehrfache Produkte erhalten wir
Beispiele
Vektoren-Metrik
besteht aus Vektoren-Metriken, d.h. 1-Formen. Das Messen passiert indem geprüft wird, wie viele Stapel durchstochen werden
Parallelogramm-Metrik
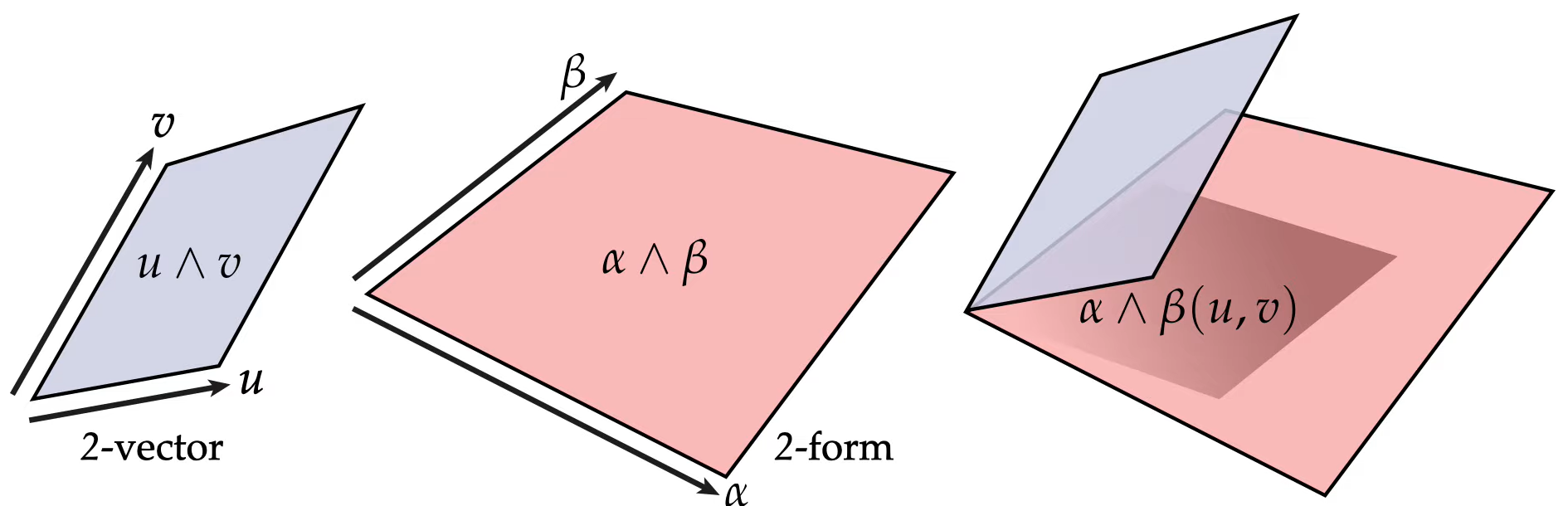
Simple Objekte aus messen Parallelogramme, die durch zwei Vektoren aufgespannt sind. Das Messen passiert, indem geprüft wird, wie viele “Ko-Parallelogramme” von dem gemessenen Paralellogramm überdeckt werden, multiliziert mit der Fläche des Koparallelogramms.
Spat-Metrik
Simple Objekte aus misst Spate, die durch drei Vektoren aufgespannt sind. Das Messen geschieht analog wie bei den Parallelogrammen.