System of autonomous linear ODEs

Description

This is a special case of the System of linear ODEs, where the matrix $A$ and the additive coefficient $b$ is constant. This allows us to solve these objects by leveraging the theory of eigenvalues and eigenvectors.

Definition

A differential equation $x^{\prime }(t)=Ax(t)+b$ with $A$ a matrix and $g$ a vector is called a system of autonomous linear ODEs. If $g$ vanishes then the system is called homogenous. Otherwise it is called nonhomogenous.

Properties

This class of equation borrows all properties of the System of linear ODEs, including the fact that the solutions form a vector space.

Phase portraits

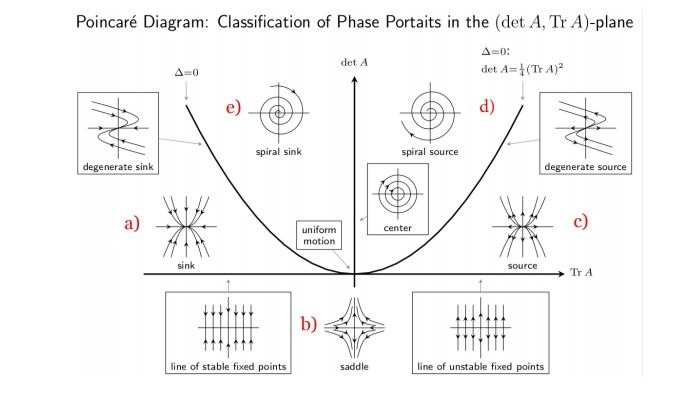
These ODEs are quite simple, so the Phase portrait of $x^{\prime }=Ax$ can be classified. This is done by doing the following:

1. If the matrix $A$ is invertible, then $0$ is the only constant solution
2. All real eigenvectors $v_i$ with real eigenvalues ${\lambda }_i$ give the ray-like solution $v_i{e}^{{\lambda }_{i}t}$. This is expanding for positive ${\lambda }_i$ and contracting for negative.
3. All imaginary eigenvalues becomes a (possibly elliptic) rotation, evident by the $sin$ and $cos$ in the solution
4. All complex eigenvalues become expansion/contraction combined with a rotation
5. All other solutions are linear combinations of the first and fill in the blanks.

The possibilities can be seen here

Stability from Eigenvalues

The solutions of $x^{\prime }=Ax$ are

1. stable if the matrix is diagonalisable and all Eigenvalues have non-positive real part
2. asymptotically stable if all eigenvalues have negative real part

Examples

Solutions of system of homogenous linear equations with constant diagonalisable matrix $A$

Let $x^{\prime }=Ax(t)$. For any Eigenvektor $v$ and Eigenwert $\lambda$ we get a solution $\mu (t)=e^{t\lambda }v$ as can be checked by hand ${\mu }^{\prime }(t)=\lambda e^{t\lambda }v=Av{e}^{\lambda t}=A\mu (t)$ If $A$ is diagonalisable then we already have $n$-solutions spanning the whole space. The give us the Fundamental system (ODE).

Solutions of system of homogenous linear equation with constant non-diagnonalisable matrix $A$

Let $x^{\prime }=Ax$. We do the following steps:

1. Calculate the Eigenwerte of $A$
2. For each eigenvalue $\lambda$ calculate the Generalised eigenvectors $v_1,...,v_k$
3. For each Eigenvalue the functions: $e^{\lambda t}{v}_1,e^{\lambda t}(v_2+v_{1}t),...,e^{\lambda t}(v_k+...+t^{k-1}{v}_1)$ are linearly independent. The whole set will give us the Fundamental system (ODE).

The solution above can simply be formalised by the Matrixexponential $e^{At}$.

Solutions of system of homogenous linear equations with complex eigenvalues (my way)

The method proposed in the book is stupid. Just calculate the eigenvalues and eigenvectors normally. It will be weird, since they are complex but when calculating $e^{tA}$ everything should cancel out and we’ll be left with real function. (since the exponential is a power series of real matrices) To calculate the solution for a given starting point. Multiply $e^{tA}$ with that point.