Periodischer Zopf

Beschreibung

Der Periodische Zopf (nicht zu verwechseln mit dem Zyklischer Zopf) ist ein Zopf, dessen realisierender Homöomorphismus der gebohrten Kreisfläche nach der Nielsen-Thurston Klassifikation periodisch ist.

Charakterisierung:

DIe untere Eigenschaft besagt, dass periodische Zöpfe konjugiert zu einer Potenz zweier Elemente ist. Für einen periodischen Zopf $\beta$ auf $n$ Strängen gilt damit ${\beta }^n=e$ oder ${\beta }^{n-1}=e$. Dies ist ein einfacher Weg, um Periodizität zu prüfen.

Eigenschaften

Endliche Ordnung

Ist der realisierende Homöomorphismus $f$ periodisch, so führt eine endliche Anwendung von $f$ zu einer Abbildung $f^n$, die isomorph zur Identität ist. Die Isomorphie erlaubt dabei die Mengenweise Rotation des Randes. Für den Zopf $\alpha$ gilt damit ${\alpha }^n={\Delta }^k,\text{ fu¨r ein }k\in \mathbb{Z}$ Nach Kérékjartó und Eilenberg ist der Zopf damit konjugiert zu einer Potenz von $\delta ={\sigma }_1...{\sigma }_{n-1}$ oder $ϵ={\sigma }_1({\sigma }_1...{\sigma }_{n-1})$.

Beweis: Es soll ein Beweis für die Form ${\delta }^k,e^k$ gegeben werden. Angenommen, der betrachtete Zopf ist periodisch im oberen Sinne. Der obere Automorphismus von der durchbohrten Kreisscheibe $D_n$ setzt sich zu einem Automorphismus der Kreisscheibe $D$ fort. Ergebnisse der Topologie konnten zeigen, dass jeder solche Automorphismus $f$ in $\text{Homeo}(D)$ konjugiert zu einer einfachen Rotation der Kreisscheibe ist. Die Bedingung der Peridiodizität sagt uns, dass die Rotation um einen rationalen Winkel rotiert. Die Rotation habe eine Ordnung von $m$. $f$ verhält sich wegen der Konjugation ähnlich. Die $n$ markierten Punkte der Kreisscheibe werden generell entlang von Orbits der Länge $m$ getauscht, es sei denn einer der Punkte liegt im Mittelpunkt der Rotation, dann ist er nämlich fix. Jeder Automorphismus der Kreisscheibe wirkt also auf folgende zwei Arten auf die $n$ Punkte. (Mehrfachanwendungen der unteren beiden Bilder sind auch erlaubt) 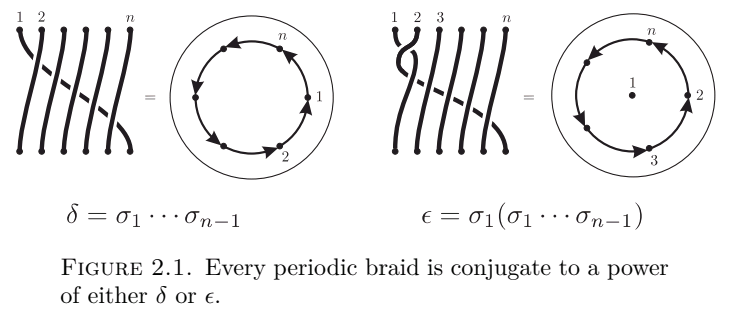Wie man sehen kann, induzieren die beiden unterschiedlichen Automorphismen unterschiedliche Zöpfe $\delta ,ϵ$.

Zentralisator

Ist der Zopf $\alpha$ periodisch, dann ist er konjugiert zu einer Potenz der Rotationen $\delta$ oder $ϵ$. Der Zentralisator des Zopfes $\alpha$ sind alle Zöpfe, die den Zopf dieser Rotation invariant lässt. Algebraisch ist der Zentralisator eine Zopfgruppe auf einem Annulus.

Bedingungen für Ordnungserhaltung

Sei $\beta$ ein Periodischer Zopf.

1. Ist $\beta$ konjugiert zu $ϵ$, so erhält der Zopf eine Ordnung auf $F_n$
2. Ist $\beta$ konjugiert zu $\delta$, so erhält der Zopf keine Ordnung

Beweis: Das ist jetzt kein Beweis aber eine Intuition. 2) ist offensichtlich war. Ordne die Erzeuger $x_1,...,x_n$ der Fundamentalgruppe ${\pi }_1(D_n)$. $\delta$ tauscht sie aus, deshalb kann kein Erzeuger am größten gewesen sein. Bei $ϵ$ funktioniert der gleiche Trick nicht. Wegen der Bohrung in der Mitte wickelt sich immer ein $x_i$ um den Mittelpunkt. Dies erlaubt uns dieses $x_i$ als den größten Erzeuger zu deklarieren. Anwendung von $ϵ$ bildet diesen dann nicht auf einen kleineren Erzeuger ab.

sicResultsBraid]]