Totale Amalgamation

Beschreibung

Sei $A$ eine Adjazenzmatrix eines Untershift endlichen Typs. Die totale Amalgamation erhält man nach einer maximal möglichen Durchführung von Amalgamationen. Je nach Typ der Amalgamation erhält man zwei Typen von totalen Amalgamationen:

• Die totale spaltenweise Amalgamation erhält man, indem man solange spaltenweise amalgamiert wie theoretisch möglich ist. Sie wird notiert durch $A_c$. Bis auf einer Permutation der Indizes ist sie wohldefiniert und eindeutig.
• Analog lässt sich für wiederholte zeilenweise Amalgamationen die sogenannte totale zeilenweise Amalgamation definieren. Diese hat dann ganz ähnliche Eigenschaften.

Eigenschaften

Bedingung für topologische Konjugation

Seien $A,B$ zwei Matrizen mit der gleichen totalen spaltenweisen Amalgamation $A_c$. Dann sind ihre einseitige Untershifts topologisch konjugiert.

Äquivalenz zur Topologischen Konjugation von einseitigen Untershifts

Seien $A,B$ irreduzible, quadratische, nicht-negative Matrizen. Zwei einseitige Untershifts $X_A,X_B$ sind genau dann topologisch konjugiert, wenn $A,B$ eine gemeinsame totale spaltenweise Amalgamation $A_c$ besitzten.

Beweis: Dieser Beweis hat einige sehr interessante Techniken, die ich mir merken sollte. Sei $\phi :X_A\to X_B$. Es ist bekannt, das topologische Konjugationen $\phi ,{\phi }^l$ invertierbare $l$-Blockabbildungen sind. Wir wollen zeigen, dass die beiden Matrizen $A,B$ die gleiche totale zeilenweise Amalgamation besitzen. Dazu reicht es aus, dass es ein $X_C$ gibt, welches durch Symbolspaltung von $A,B$ hervorgeht. Umkehrung der Spaltung (also Amalgamation) und die Kommutativität von Amalgamationen zeigt, dass die totale Amalgamation gleich ist. Wir definieren $X_C$, indem wir die $\phi$ durch seine Wirkung auf $l$-lange Wörter charakterisieren. Konkret definiere das Alphabet: $L_C=\{([x_0,...,x_{l-1}],[y_0,...,y_{l-1}]):\phi (x)=y\}$ Definiere die Transition. Das Symbol $([z_0,...,z_{l-1}],[w_0,...,w_{l-1}])$ kann $([x_0,...,x_{l-1}],[y_0,...,y_{l-1}])$ folgen, wenn die Blockpräsentationsbedingung $z_{i-1}=x_i,w_{i-1}=y_i$ erfüllt ist. Blickt man auf das definierte Alphabet, ergibt es Sinn, dass die Zeichen $([x_0,...,\ast ],[\ast ,...,\ast ])$ durch Symbolspaltung aus $x_0$ hervorgehen und die Zeichen $([\ast ,...,\ast ],[y_0,...,\ast ])$ durch Symbolspaltung aus $y_0$ hervorgehen. Das folgt einem ähnlichen Induktionsargument wie als man zeigen sollte, dass höhere Blockpräsentationen Symbolspaltungen sind. $\square$

Äquivalenz zur Topologischen Konjugation von zweiseitigen Untershifts

Seien $A,B$ irreduzible, quadratische, nicht-negative Matrizen. Zwei einseitige Untershifts ${\Sigma }_A,{\Sigma }_B$ sind genau dann topologisch konjugiert, wenn es eine quadratische, nicht-negative Matrix $C$ gibt, sodass

• $A,C$ haben eine gemeinsame totale spaltenweise Amalgamation $A_c$
• $B,C$ haben eine gemeinsame totale zeilenweise Amalgamation $A_r$

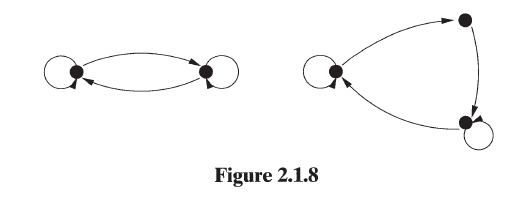
Interessanterweise ist die Bedingung bei zweiseitigen Untershifts einfacher zu erfüllen. Trotzdem ist es schwieriger zu zeigen. Bis heute weiß man nicht, ob es einen Algorithmus gibt, der zeigt, ob die die Untershifts topologisch konjugiert sind. Es gibt also Beispiele von Matrizen, deren einseitigen Shifts konjugiert sind, deren zweiseitigen Shifts aber nicht. Wie dieses hier:

tchensSymbolicDynamicsOnesided2012]]