Beschreibung
Eine Reelle Zahl ist irrational, wenn sie nicht rational ist.
Beispiele
Wurzel 2
ist irrational. Dazu gibt es einen langweiligen Wiederspruchsbeweis, den man in der Schule macht und einen coolen Beweis durch Euklidische Konstruktion.
Beweis: (von Apostol)1 Zeige: ist irrational. lässt sich als die Hypothenuse eine rechtwickligen, gleichschenkligen Dreiecks (mit Katheten 1) konstruieren.
Angenommen, wäre rational, hätte also die Form . Dann könnte man das Dreieck um den Faktor skalieren. Man erhält ein Dreieck, dessen Seiten natürliche Zahlen sind.
Wir haben durch Angabe eines Beispiels die Existenz von Dreiecken gezeigt, deren Seiten natürliche Zahlen sind. Sei das kleinste Dreieck mit der Eigenschaft. (Dreieck in der Skizze links). In dieses Dreieck können wir nun ein noch kleineres Dreieck konstruieren.
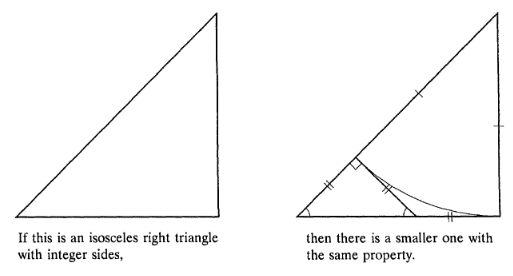 Dieses Dreieck hat aber auch Längen natürlicher Zahlen! Somit ist das vorhin gewählte Dreieck nicht das kleinste, es entsteht ein Widerspruch.
Dieses Dreieck hat aber auch Längen natürlicher Zahlen! Somit ist das vorhin gewählte Dreieck nicht das kleinste, es entsteht ein Widerspruch.