Braid group

Beschreibung

Die Menge aller Zöpfe ergibt eine Gruppe, die wir als Zopfgruppe bezeichnen. Zöpfe haben viele Charakterisierungen, diese ergeben ebenso viele Möglichkeit, eine Gruppe auf den Zöpfen zu definieren. Dieser Artikel befasst sich hautsächlich mit den gruppentheoretischen Eigenschaften von Zöpfen. Dynamische Eigenschaften findet man eher im Artikel Zopf.

Definition als Partikelbewegung

Seien $z(t),z^{\prime }(t)$ zwei Zöpfe, mit den gleichen Endpunkten und Startpunkten, d.h. $\{z_1(0),...,z_n(0)\}=\{z_1^{\prime }(0),...,z_n^{\prime }(0)\}$. Dann kann man diese Konkatenieren.

Die Konkatenation definiert die Artin Zopfgruppe auf $n$-Strängen.

Definition als Konfigurationsraum

Zöpfe können als Homotopieklassen des Konfigurationsraumes $K(\mathbb{C},n)$ betrachtet werden. Die Zopfgruppe ist damit gleich der Fundamentalgruppe.

Definition als Abbildungsklasse

Ein Zopf ist eine Isotopieklasse von Homöomorphismen der durchbohrten Kreisscheibe $D_n$fe ist durch die Abbildungsklassengruppe gegeben: $\text{Mod}(D_n)={\text{Homeo}}^{+}(D_n)/{\text{Homeo}}_0^{+}(D_n)$

Definition als Automorphismus

Zöpfe si der freien Gruppe. Als solche bilden sie durch Multiplikation eine Gruppe.

Definition durch Präsentation

Zöpfe erfüllen des Weiteren die Relationen der Artin-Darstellung

• ${\sigma }_j{\sigma }_k={\sigma }_k{\sigma }_j$ für $|j-k|>1$
• ${\sigma }_j{\sigma }_k{\sigma }_j={\sigma }_k{\sigma }_j{\sigma }_k$ für $|j-k|=1$

Wir erhalten Zopfgruppen durch die Präsentation oberer Generatoren und Relatoren.

Beweis: Dieser Beweis wird einmd)aber da es hier um das Zeigen einer Präsentation geht, ist das für meine Zukunft als geometrischer Gruppentheoretischer wichtig. Wir wollen zwei Sachen zeigen:

• Die Zopfgruppe hat obige Relationen (eigentlich klar)
• Die Zopfgruppe braucht nur diese Relationen

Letzteres zeigen wir folgendermaßen: Angenommen, wir haben ein Wort in $W={\sigma }_{i_1}^{e_1}...{\sigma }_{i_m}^{e_m}$ dessen Zopf trivial ist. Wir zeigen, dass wir ein triviales Wort erhalten können, indem wir nur die oberen Relatoren verwenden. Für den Beweis nutzen wir die Tatsache, dass der triviale Zopf rein ist. Wegen der gespaltenen, exakten Sequenz $F_n\to P{B}_n\to P{B}_{n-1}$ ist jeder Reine Zopf eindeutig als $W=f\cdot p$. darstellbar, wobei $f\in F_n,p\in P{B}_{n-1}$. Dadurch können wir das Problem induktiv vereinfachen. $P{B}_n$ hat die obige Presentation, wenn $P{B}_{n+1}$ die obige Präsentation hat. Wir werden eine solche Zerlegung angeben und die Eindeutigkeit der Zerlegung ausnutzen. Für $0,...,m$ sei $j_k$ die Position des $n$-ten Fadens nach der Bewegung ${\sigma }_{i_1}^{e_1}...{\sigma }_{i_k}^{e_k}$. Da $W$ trivial ist gilt offenbar $j_0=j_m=n$. Sei ${\alpha }_i={\sigma }_i...{\sigma }_{n-1}$ eine Bewegung, die den Faden $i$ auf $n$ schickt. $W$ kann nun geschrieben werden als $W=({\alpha }_{j_0}^{-1}{\sigma }_{i_1}^{e_1}{\alpha }_{j_1})...({\alpha }_{j_{m-1}}^{-1}{\sigma }_{i_1}^{e_m}{\alpha }_{j_m})$ Je nachdem, wie der mittlere Term auf die Position des $n$-ten Fades wirkt, kann jeder geklammerte Term kann nun geschrieben werden als:

1. $({\sigma }_{n-1}^{-1}...{\sigma }_i^{-1}){\sigma }_i({\sigma }_{i+1}...{\sigma }_{n-1})=e$
2. $({\sigma }_{n-1}^{-1}...{\sigma }_i^{-1}){\sigma }_i^{-1}({\sigma }_{i+1}...{\sigma }_{n-1})=:x_i^{-1}$
3. $({\sigma }_{n-1}^{-1}...{\sigma }_i^{-1}){\sigma }_{i-1}({\sigma }_{i-1}...{\sigma }_{n-1})=:x_{i-1}$
4. $({\sigma }_{n-1}^{-1}...{\sigma }_i^{-1}){\sigma }_{i-1}({\sigma }_{i-1}...{\sigma }_{n-1})=e$
5. $({\sigma }_{n-1}^{-1}...{\sigma }_i^{-1}){\sigma }_k^{\pm 1}({\sigma }_i...{\sigma }_{n-1})={\sigma }_k^{\pm 1}$ für $k<i-1$, da ${\sigma }_k^{\pm 1}$ mit den anderen Sachen kommutiert.
6. $({\sigma }_{n-1}^{-1}...{\sigma }_i^{-1}){\sigma }_k^{\pm 1}({\sigma }_i...{\sigma }_{n-1})={\sigma }_{k-1}^{\pm 1}$ für $k>i$ nach Anwendung der oberen erlaubten Relatoren.

Wir streben eine Zerlegung $F_n⋊B{P}_{n-1}$ an. Die $x_i$ sind daher so gewählt, dass sie isomorph zur Fundamentalgruppe sind, die man bekommt, wenn man den $n$-ten Faden um alle anderen wickelt. Als nächstes soll das Wort als Produkt der beiden Gruppen geschrieben werden. Dazu wollen wir wissen, wie $B{P}_{n-1}$ durch Konjugation auf Elementen von $F_n$ wirkt: Wir beobachten, dass für $i=1,...,n-2$ und $j=1,...,n-1$ gilt: ${\sigma }_i^{-1}{x}_j{\sigma }_i=x_{i+1}{x}_i{x}_{i+1}^{-1}$. Für $i=j$ gilt sogar ${\sigma }_i^{-1}{x}_j{\sigma }_i=x_{i+1}$ und für $i>j$ gilt ${\sigma }_i^{-1}{x}_j{\sigma }_i=x_i$.

Wir nutzen jetzt die Regeln 1-6 und schreiben das Wort um. Dann nutzen wir die Konjugationsregeln, um alle $\sigma$ nach rechts zu schieben, sodass wir die gewünschte Zerlegung $W=fp$ erhalten. Da $W$ trivial ist, evaluiert auch $f$ und $p$ als trivial. $f$ ist ein Element ein Element der freien Gruppe und damit genau dann trivial, wenn $f$ das neutrale Element ist. $p$ ist ein Element der kleineren Zopfgruppe $P{B}_{n-1}$. Durch Induktion kann man zeigen, dass die oberen Relationen ausreichen, um zu zeigen, das das Wort trivial ist.

Beweis 2: Es gibt ein topologischeres Argument, das die oberen Relationen als natürlich aussehen lässt. Das Argument ist außerdem etwas schöner. Es ist bekannt, das ein Zopf die Fundamentalgruppe von $K(\mathbb{C},n)$ ist. Wir können außerdem die Präsentation von Fundamentalgruppen von regulären $m$-Zellkomplex berechnen, aus denen $m-2$-Komplexe herausgeschnitten sind. Das bringt uns auf die Idee, einen $m$-Zellkomplex $C$ zu konstruieren, der nach dem Entfernen eines $m-2$-Komplexes $C^{\prime }$ homöomorph zu $K(\mathbb{C},n)$ wird. Dann können wir die Präsentation explizit errechnen. Wir betrachten den Raum von $n$-ungeordneten Punkten $C={\mathbb{C}}^n/{\Sigma }_n$. Wir statten diesen nun mit einem Skelett aus. Dieses ist durch eine (lexikographische) Ordnung definiert. Für zwei komplexe Zahlen ist $z_1<z_2⟺Re(z_1)<Re(z_2)$ und $z_1⊻z_2⟺Re(z_1)=Re(z_2)\wedge Im(z_1)<Im(z_2)$. Eine Folge von Symbolen $=,<⊻$, z.B. $\theta =(=,<,=,...,⊻)$ definiert nun eine Zelle $C_{\theta }=\{\{z_1,...,z_n\}\in C:z_1=z_2<z_3=...⊻z_n\}$Die Dimension der Zelle ist gegeben durch die Art der verwendeten Symbole.$di{m}_{\mathbb{R}}(C_{\theta })=2n-{\#}_{⊻}-2{\#}_{=}$Zum Beispiel ist der Raum, wo zwei Punkte gleich sind (also ein $=$) enthalten ist, eine $m-2$-dimensionale Zelle. Die Vereinigung der Abschlüsse dieser Zellen ist die Große Diagonale $C^{\prime }$. Entfernt man die, erhält man we gewünscht einen Konfigurationsraum $C\backslash C^{\prime }\cong K(\mathbb{C},n)$. Wir können nun die Generatoren und Relatoren errechnen. Die einzige $m$-Zelle ist $C_{(<,...,<)}$. Jede Kante ist also eine Schleife und damit nicht im dualen Baum enthalten. Damit ist jeder $m-1$-Komplex ein Generator. Die $m-1$ Komplexe sind durch die $2n$ Folgen ${\theta }_i$ gegeben, bei denen das $i$-te Symbol das $⊻$ ist. Eine Schleife die nur $C_{{\theta }_i}$ durchstößt korrespondiert mit einem Tausch der Punkte $i$ und $i+1$. Der Generator ist also genau der Standarderzeuger ${\sigma }_i$! Die Relatoren erhält man durch das Betrachten von Loops um $m-2$-Komplexe. Da wir alle Komplexe mit $=$ entfernt haben, können die übrigbleibenden nur durch zwei $⊻$ definiert sein. Wir unterscheiden:

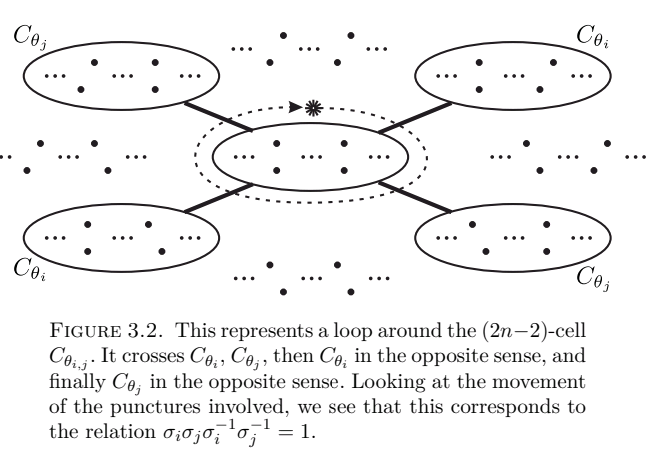
• $\theta =(<,...,<,⊻,<,...,<,⊻,<,...,<)$: Eine Skizze zeigt, dass man zur Umrundung erst $C_{{\theta }_i}$ und $C_{{\theta }_j}$ und dann $C_{{\theta }_i}$, $C_{{\theta }_j}$ in Rückrichtung durchstößt. Daraus ergibt sich ein Relator ${\sigma }_i{\sigma }_j{\sigma }_i^{-1}{\sigma }_j^j=1$
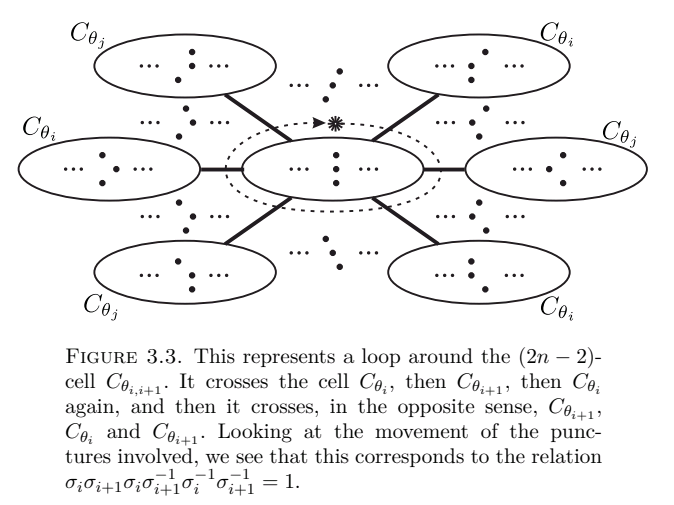
• $\theta =(<,...,<,⊻,⊻,<,...,<)$: Eine weitere Skizze zeigt, dass zur Umrundung die zwei Zellen dreimal durchstoßen werden müssen. Es ergibt sich der Relator ${\sigma }_i{\sigma }_{i+1}{\sigma }_i{\sigma }_{i+1}^{-1}{\sigma }_i^{-1}{\sigma }_{i+1}^{-1}$.

Eigenschaften

Lösbares Wortproblem

Das Wortproblem (Gruppe) ist lösbar, d.h. für zwei Zöpfe ${\beta }_1,{\beta }_2$ kann festgestellt werden, ob sie gleich sind.

**B).md)dem man einen Zopf als Standard-Erzeuger schreibt, und diese in einen Automorphismus der freien Gruppe umwandelt. Zwei Automorphismen sind gleich, wenn sie gleich auf den Erzeugern wirken. Dies ist leicht (wenn auch nicht effizient) zu berechnen.

Beweis 2: Alternativ schreibt man ein Wort in die Linksnormalform. Dann kann man die Worte vergleichen.

Lösbares Konjugationsproblem

Es gibt einen Algorithmus mit dem man feststellen kann, ob zwei Wörter zueinander konjugiert sind. Ein neuer Algorithmus für den $3$-Zopf basiert auf Zugstrecke der dreifach punktierten Kreisscheibe

Abbildungsklassengruppe der durchbohr h zur Abbildungsklassengruppe $\text{Mod}(D_n,\partial D_n)$ der Durchbohrte Kreisscheibe, die den Rand punktweise fix lässt

Residuell endlich und hopsch

Zopfgruppen sind Residuell Endliche Gruppe und Hopfsche Gruppe

Exakte S ppe.m20Gruppe.md)er Zopf|Reine Zopfgruppe]] und die Symmetrische Gruppe in Verbindung bringt.

$1\to P{B}_n\to B_n\to {\Sigma }_n\to 1$

Torsionsfreiheit

Zöp Gruppe]]

Beweis 1: Ein zyklischer Zopf ist ein zyklisches Element der Abbildungsklassengruppe. Damit ist er im Besonderen ein Periodischer Zopf im Sinne der Thurston-Nielsen-Klassifikation. Als solches ist er konjugiert zu einer Potenz von $\delta ={\sigma }_1...{\sigma }_{n-1}$ oder $ϵ={\sigma }_1({\sigma }_1...{\sigma }_{n-1})$. Für diese beiden Elemente gilt jedoch ${\delta }^n={\Delta }^2={ϵ}^{n-1}$. Die beiden Zöpfe haben damit offensichtlich keine endliche Ordnung.

Beweis 2: Viel einfacher ist folgender Beweis. Wir wissen, dass $B_n$ eine Links-Ordnung zulässt. Damit ist sie torsionsfrei.

Beweis 3: Dieser Beweis nutzt die Präfix-Ordnung (Zopf). Angenommen $x^n=1$ für einen Zopf $x\in B_n$. Betrachte $d=1\wedge x\wedge ...\wedge x^{n-1}$. Dann gilt auch $xd=x\wedge x^2\wedge ...\wedge x^n=d$. Teilt man $d$ heraus, erhält man $x=1$.

Links-Ordnung

Zopf-Gruppen sind Links-Geordnete Gruppe. Eine typische Ordnung ist Dehornoys Ordnung

Linearitä e.md)uppe|Linear]]. D.homorphismus]] $\rho :B_n\to G{L}_N(k)$, wobei $k=\mathbb{Q}(p,q)$ und $N=n(n-1)/2$

ltBraidsDynamics2022]] lit_kinBraidsOrderingsMinimal2018 lit_BasicResultsBraid