Beschreibung
Die Differentialform von Grad ist eine Interpretation der Ableitung, die vor allem Anwendung im Studium von Differenzierbaren Mannigfaltigkeiten hat. Daher ist auch der wichtigere Artikel dieser hier: Differentialform (Mannigfaltigkeit).
Sie funktioniert, indem sie jedem Punkt eines Raumes eine -Form zuordnet. Die -Formen können dann als Volumenfunktionen betrachtet werden. Sie beschreiben nämlich, welches Volumen ein Parallelogramm hat, dass durch zwei Vektoren aufgespannt ist. Diese Volumenfunktion darf über den betrachteten Raum variieren, d.h. unterschiedliche Gewichtungen erlauben.
Hier soll auf die Intuition der Differentialform im euklidischen Raum eingegangen werden.
Definition
Eine Differentialform von Grad auf dem euklidischen Raum ist eine Zuordnung woe Form|Form]] ist, die sich glatt mit verändert.
*Das Analogon zu der oberen Zuordnung ist der Schnitt (Vektorbündel) *
Eigenschaften
Basis der Differential- -Form
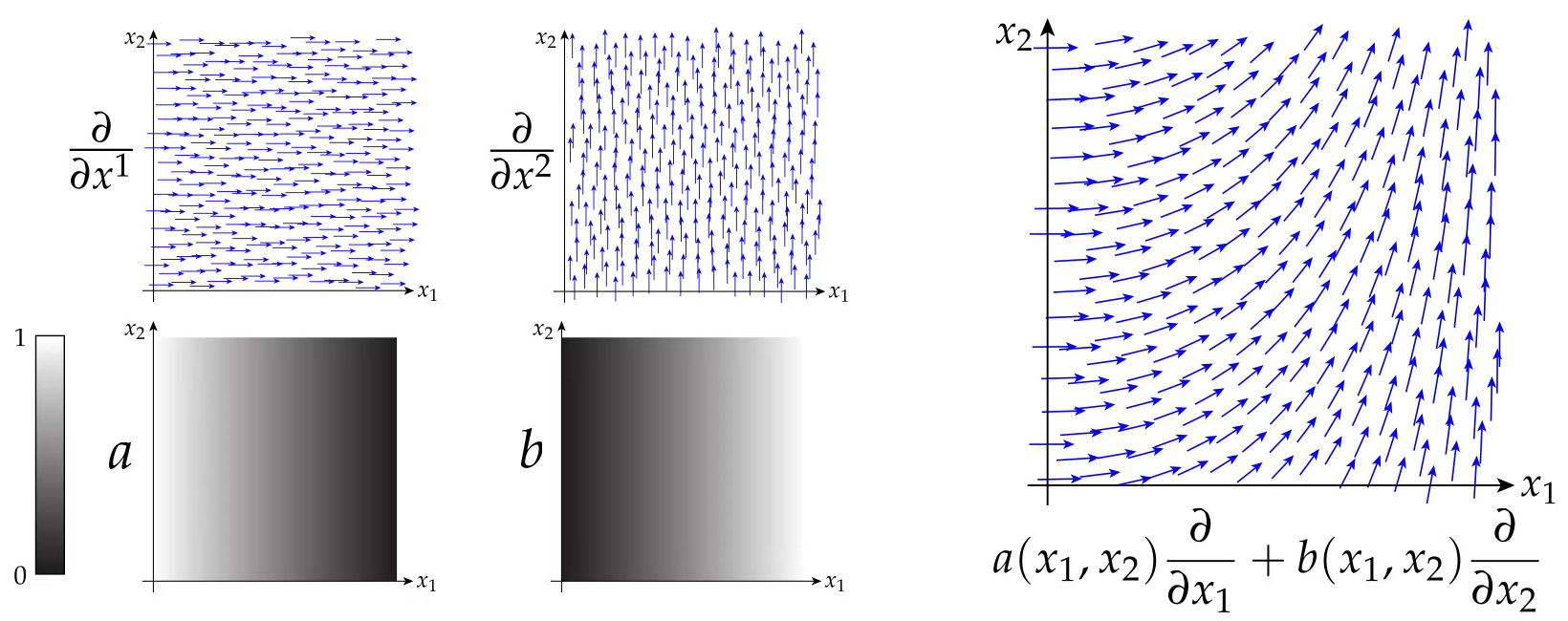
Wir bezeichnen mit die -Formen, die in Richtung der -Standardbasis zeigen. Diese Formen bilden eine Basis von . Jede andere Differentialform lässt sich also als eine (punktweise) Linearkombination schreiben:
sind dabei glatte Funktionen.
Die Bezeichnung ist erstmal ausschließlich symbolisch zu betrachten. Irgendeine Verbindung zu Ableitungen zu erstellen führt zu viel zu vielen Kopfschmerzen.
Beispiele
Differentialform von Grad
Diese Differentialform ordnet jedem Punkt eines Raumes einen Skalar aus zu.
Differentialform von Grad
Diese Differentialform ordnet jedem Punkt eines Raumes einen -1-Form zu. Das lässt sich visualisieren als eine Höhenkarte. Die Differentialform frisst einen Tangentenvektor überall und misst, wie steil es nach oben geht.