Beschreibung
Die Lokale Geodätische der Kugel ist die längenrealisierende Kurve auf der Kugel, d.h. der Sphärische Geometrie.
Definition
Die geodätischen Kurven sind die Kurven mit Länge , die Teile eines Großkreises sind.
Beweis: Eine Ebene, die parallel zur Tangentialebene eines Punktes steht teilt die Kugel in zwei Teile. Einen inneren Teil, der enthält und einen äußeren Teil, der nicht enthält.
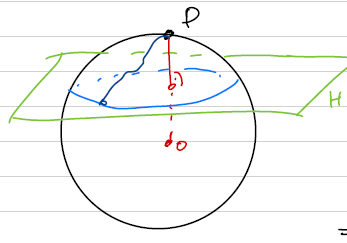
Der Schnitt von der Ebene und der Kugel ist ein Kreis. Alle Punkte darauf haben den gleichen Abstand von , da die Rotation eines Punktes auf dem Kreis um die Achse die durch und seine Antipode verläuft, eine Isometrie ist. Nenne diesen Abstant
Alle Punkte im Inneren haben Abstand und alle Punkte im äußeren .
Wir nehmen nun Punkte und suchen die kürzeste Kurve zwischen den beiden. Wir nehmen an der Winkel zwischen ist spitz.
Wir finden nun wieder Ebenen Parallel zur Tangentialebene aber so, dass sich die beiden Ebenen auf einem Punkt auf dem Großkreis, der durch und verläuft, schneiden.
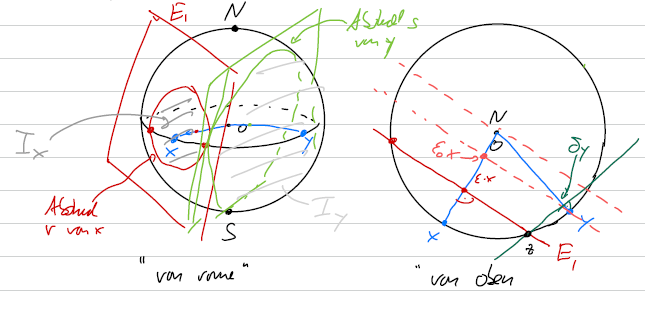Das ganze kann man auch von oben betrachten. Bezeichne mit die Abstände von zu den Kreisen. Da die beiden Inneren Teile offen und disjunkt sind, muss man, um von zu zu gelangen, erst das Innere um verlassen und dann das Innere um betreten. Für eine Kurve , die das tut gilt also . Da am Rand beider Inneren ist gilt . Also muss die Längenrealisierende Kurve durch verlaufen.
Wir können jetzt die grüne Ebene beliebig nah an oder heranbewegen. Das als Schnittpunkt beider Ebenen durchläuft dann alle auf dem Großkreissegment zwischen und . Also muss eine längenrealisierende Kurve das Großkreissegment enthalten. Das Großkreissegment ist aber schon die kleinste Kurve, die das Segment enthält, wodurch gezeigt ist, dass längenrealisierende Pfade Groskreissegmente sind.
Wie der Beweis für stumpfe Winkel geht weißt ich nicht. Entweder mit negativen oder durch das Teilen vom stumpfen Winkel in zwei spitze.