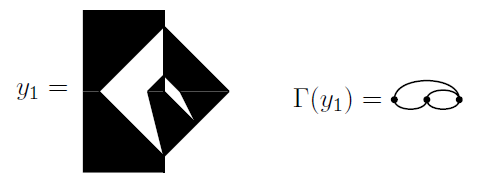Orientierte Thompsongruppe

Beschreibung

Johnson hat festgestellt, dass man aus Elementen der Thompsons Gruppe F jede Verschlingung erstellen kann. Diese Verschlingungen besitzen jedoch keine natürliche Orientierung. Glücklicherweise existiert eine Untergruppe der Thompsonuntergruppe, deren Elemente auf natürliche Weise orientierte Verschlingungen induzieren.

Definition

Sei $g=(T_{+},T_{-})\in F$. Wir definieren den planaren Graphen $\Gamma (T_{+},T_{-})$ auf die folgende Weise:

1. Wende die Inklusion nach $F_3$ an, indem eine mittlere Kante erzeugt wird.
2. Betrachte den neuen Graphen $(T_{+},T_{-})$, nun mit mittleren Kanten.
3. Färbe die Flächen weiß und schwarz ein, die äußere Komponente links ist dabei schwarz und die rechts ist weiß. Dies ist immer wohldefiniert.
4. Erstelle den planaren Graphen, indem jeder schwarze Bereich zu einem Knoten gemacht wird. Zwei schwarze Bereiche sind durch eine Kante verbunden, wenn sie sich berühren.

Die orientierte Thomsonuntergruppe $\overrightarrow{F}\subseteq F$ bzw. ${\overrightarrow{F}}_3\subseteq F_3$ besteht aus allen Elementen deren planare Graphen $2$-Färbbar sind. (bei Elementen $g\in F$ wenden wir erst die Inklusion in $F_3$ an) Bei den Färbungen nutzen wir die Konvention, dass der Knoten ganz links die Farbe $+$ hat.

Jetzt, wo jeder Knoten des planaren Graphen eine Orientierung hat, kann man den Medialgraph zeichnen. Die Orientierung der Verschlingungssegmente geht im Urzeigersinn um $+$-Knoten und gegen den Uhrzeigersinn für $-$-Knoten

Definition: Generator

Die Ternäre orientierte Thompsongruppe ${\overrightarrow{F}}_3$ ist generiert durch die Elemente $⟨y_{2i+1}^2,y_2,y_{2i+2},y_{2i}{y}_{2i+3}:i=0,1,2⟩$

Eigenschaften

Eigenschaft