Beschreibung
Es ist möglich eine Präsentation als planaren Grahp darzustellen. Wir färben dazu jede zweite Zusammenhangskomponente grau ein, sodass die äußere Komponente weiß bleibt. Dass dies immer möglich ist, lässt sich dadurch zeigen, dass man durch Änderung der Übergänge jede Präsentation trivial machen kann, Reidemeister Bewegung die Einfärbbarkeit nicht behindern und dass der triviale Knoten offensichtlich derart einfärbbar ist. Wir setzen nun in jeder grauen Region einen Knoten (im Sinne der Graphentheorie). Zwei Knoten sind verbunden, wenn sie sich eine Kreuzung teilen. Wir zeichnen bei mehreren Kreuzungen Mehrfachkanten.
Die Unter- und Überführungsinformationen kodieren wir ein, indem wir jede Kante je nach Kreuzungstyp mit oder beschriften.
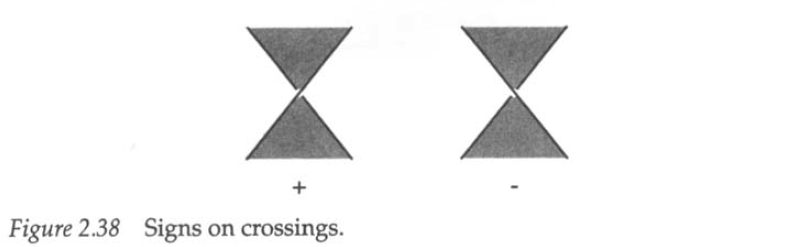
Der Knotengraph erlaubt uns, Knotenprobleme in Graphentheoretische Probleme umzuwandeln. Zum Beispiel könnte ich damit Knotentheorie und Symbolische Dynamik verheiraten. <3
Eigenschaften
Untersuchung durch Symbolische Dynamik
Man könnte den Graphen mithilfe von symbolischer Dynamik untersuchen. Vielleicht kann man da interessante Eigenschaften feststellen.