Teilring

Beschreibung

Ein Teilring ist eine Untermenge eines Ringes, welcher ebenfalls ein Ring ist und das gleiche 1-Element hat.

Definition

Sei $R$ ein Kommutativer Ring. Eine Teilmenge $S\subset R$ wird Teilring von R genannt, wenn $1_R\in S$ gilt und mit $a,b\in S$ jeweils auch die Elemente $a-b$ und $ab$ in $S$ liegen.

Durch das $a-b$ spart man sich das Prüfen der Inversen und Abgeschlossenheit.¹

Man schreibt $R|S$

Wahrscheinlich um auszudrücken, dass $R$ ein Erweiterungsring von $S$ ist. Die Schreibweise ähnelt sehr der Schreibweise der Teilbarkeit. Ich sollte Herr Gerkmann fragen, ob es da einen Zusammenhang gibt.

Das Gegenstück eines Teilrings wird Erweiterungsring genannt.

Eigenschaften

Vereinigung von Teilringen

Sei $(R,+,\cdot )$ ein Ring, und sei $(S_i{)}_{i\in I}$ eine Familie von Teilringen. Dann ist auch $S={\bigcap }_{i\in I}{S}_i$ ein Teilring von $R$

Übungen

Zahlentheorie Klausur 2019 Aufgabe 2

a)

• $R\subseteq \mathbb{R}$
• $1$ ist $1$-Element.
• $\frac{a}{5^n}+\frac{b}{5^m}=\frac{5^{m}a+5^{n}b}{5^{nm}}\in R$
• $\frac{a}{5^n}\ast \frac{b}{5^m}=\frac{ab}{5^{nm}}\in R$

b)

Zeige erst $\subseteq$: Sei $\frac{a}{5^n}\in R⟹a(\frac{1}{5}{)}^n\in \mathbb{Z}[\frac{4}{5}]$, denn $\frac{1}{5}=1-\frac{4}{5}⟹R\subseteq \mathbb{Z}athbbZ[\frac{4}{5}]$.

Zeige $\supseteq$: $\mathbb{Z}\subseteq R$ und $\frac{4}{5}\in R⟹\mathbb{Z}athbbZ[\frac{4}{5}]\subseteq R$

Zth Klausur 2018 Aufgabe 2

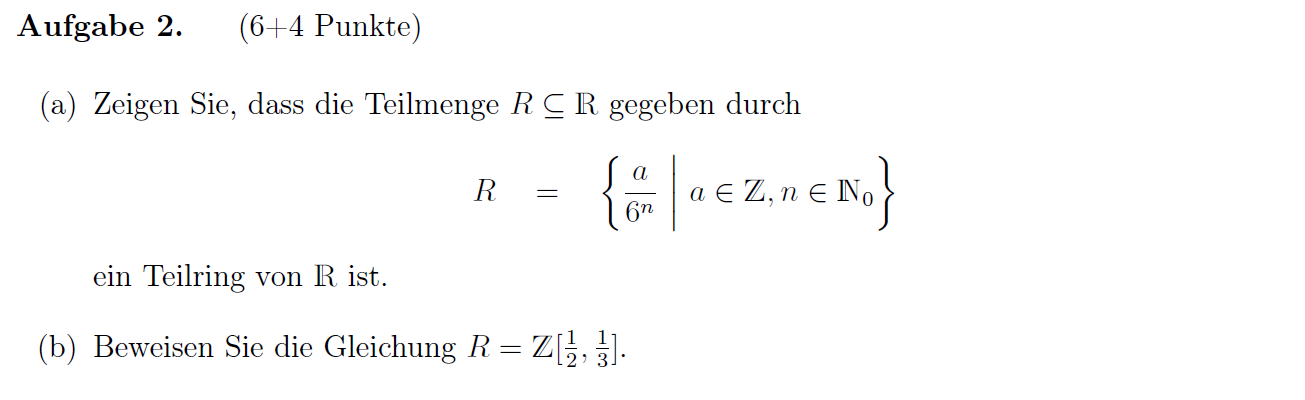
a)

Offensichtlich gilt $R\subseteq \mathbb{R}$. $R$ ist ein Ring, denn:

• $0,1\in R$ sind das Null/Einselement
• Es gilt $\frac{a}{6^n}-\frac{b}{6^m}=\frac{a{6}^m-b{6}^n}{6^{nm}}\in R$
• Es gilt $\frac{a}{6^n}\cdot \frac{b}{6^m}=\frac{ab}{6^{nm}}\in R$

$R$ und $\mathbb{R}$ haben das gleiche $1$-Element.

b)

• $\supseteq :\frac{1}{6}=\frac{1}{2}\cdot \frac{1}{3}\in \mathbb{Z}[\frac{1}{2},\frac{1}{3}]⟹\frac{a}{6^n}\in \mathbb{Z}[\frac{1}{2},\frac{1}{3}]⟹R=\mathbb{Z}[\frac{1}{2},\frac{1}{3}]$
• $\subseteq :\frac{1}{2}=\frac{3}{6}\in \mathbb{Z}[\frac{1}{2},\frac{1}{3}]$ und $\frac{1}{3}=\frac{2}{6}\in \mathbb{Z}[\frac{1}{2},\frac{1}{3}]$

\newcommand{\R}{\mathbb R}

hlentheorie

Footnotes

1. Gerkmann Satz 3.2 ↩