Beschreibung
Der Satz von Alexander ist ein Satz aus der Knotentheorie. Er besagt, dass jede Verschlingung der Abschluss eines Zopfes ist.
Es gibt einen Analogen Satz, der besagt, dass jeder Knoten asu einer Konstruktion eienes Elements der Thompsons Gruppe F realisierbar ist.
Beweis: Sei eine Verschlingung. Folge der Verschlingung entlang einer gewählten Orientierung. Setze Punkte an den Stellen zwischen einer Überführung und Unterführung. Dadurch wird die Verschlingung in maximale Brücken und maximale Tunnel unterteilt.
Verzerre die Verschlingung so, dass die Tunnel parallel zueinander sind. Die Brücken können dann komplizierte Muster bilden, schneiden sich aber nicht gegenseitig.
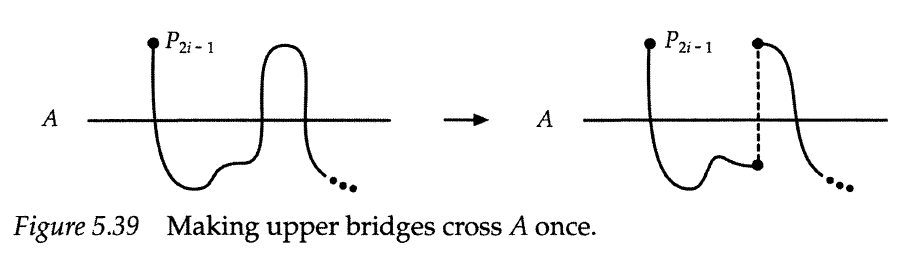
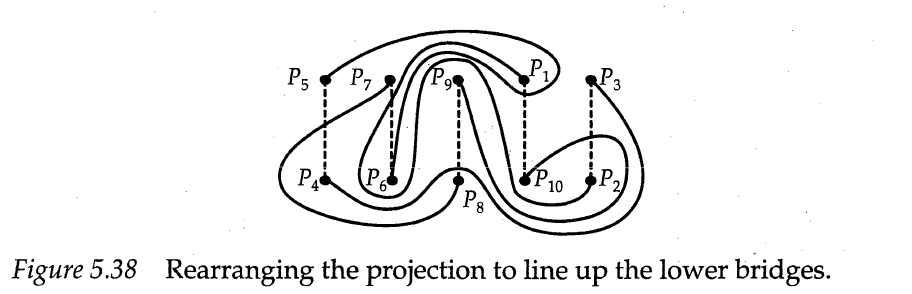Wir betrachten jetzt die einzelnen Brücken. Sie überqueren eine mittlere horizontale Linie eine ungerade Anzahl. Wir wollen, dass die Brücken die mittlere Linie nur einmal überquert. Dazu schieben wir einen Teil nachunten, wodurch ein neuer Tunnel entsteht.
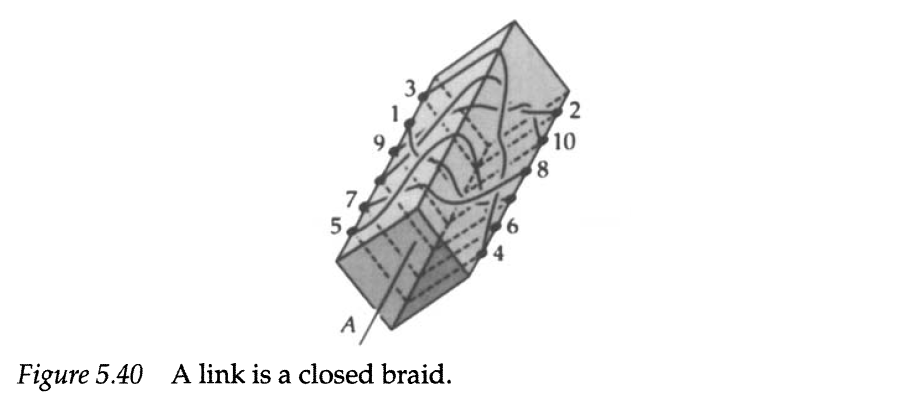Wir wickeln zuletzt die Brücken und Tunnel um eine Achse. Wie beginnen dazu bei einem Punkt und deformieren die Kurve, sodass es eine Verbindung zu ist. Dann wandern wir über einen Tunnel zu . Dort deformieren wir die nachfolgende Kurve auf die vorherige drauf. Wiederholt man die Prozedur, erhält man folgendes Bild
Eigenschaften
Eigenschaft