Beschreibung
Wenn endlich ist, kann man dann eine gute Klassifikation aller Möglichkeiten finden?
Herangehensweise
Untersuchen der Rotationspunkte
Bei einer Rotation um eine Gerade, die durch verläuft gibt es zwei Punkte auf der Einheitskugel, die Fixpunkt sind.
Untersuchen des Orbits der Rotationspunkte
Der Orbit eines Rotationspunkt nach oberer Definition besteht nur aus anderen Rotationspunkten. Das heißt, alle möglichen Rotationspunkte einer Rotation von zerfallen in Orbits.
Man kann zeigen, dass es maximal drei dieser Orbits geben muss.
Bezeichne alle Orbits mit , . Aufgrund des Orbit-Stabilisator-Satz gilt für einen Rotationspunkt . Da die Gruppe, die fix hält eine Rotation, d.h. eine Zyklische Gruppe einer Ordnung ist
Wir können damit eine Gleichung aufstellen, die starke Einschränkungen für Orbitsliefert: Definiere: Jede Rotation außer hat zwei Fixpunkte, damit gilt Jeder Rotationspunkt des Orbits hat außerdem Rotationen, die fix lassen. Damit gilt: Gleichsetzen und vereinfachen gibt, die mächtige Gleichung: , also . Außerdem kann man zeigen .
Diese Gleichung ist auch deshalb mächtig, weil wir damit durch Einsetzen der Orbitgleichungen herausfinden können, wie groß die Gruppe sein muss.
Klassifikation Stabilisatorgrößen
Wir können zeigen, dass die Orbits nur (mit Vertauschung) ganz bestimmte Größen haben können. Diese sind:
| 2 | 2 | beliebig |
| 2 | 3 | 3 |
| 2 | 3 | 4 |
| 2 | 3 | 5 |
Klassifikation
Wir verwenden nun die Klassifikation der oeren Orbits, um geometrische Objekte zu finden, die diesen Objekten entsprechen.
2 Orbits von Rotationspunkten
Nach oberer Gleichung gilt dann und damit Die Orbits sollen nicht leer sein, d.h. . Die Orbits sind die Antipoden einer einzigen Rotation. muss folglich eine endliche zyklische Gruppe sein.
Orbitgrößen 2-2-n
Einsetzen in die Gleichung ergibt also Da hat gilt und .
Damit gibt es eine Rotation, die die Punkte des Orbit (notwendigerweise aus Antipoden bestehend) vertauscht. Außerdem gibt es Rotationen, die Punkte von fix lassen. muss daher die Diedergruppe eines regelmäßigen n-Ecks sein.
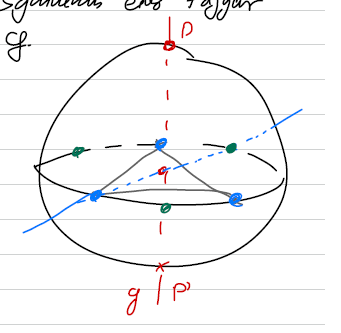
Stabilisatorgrößen 2-3-3
Einsetzen der Stabilisatorgleichungen in die obere Gleichung ergibt
, d.h. es gibt eine Rotationsgruppe um einen Punkt gibt, die Ordnung hat. Da gibt es einen anderen Punkt, der nicht und nicht sein Antipodalpunkt ist. Indem man den Stabilisator auf diesen Punkt anwendet, erhält man zwei weitere Punkte mit dem gleichen Abstand dazwischen.
Da der gewählte Punkt willkürlich ist, gilt die Winkeleigenschaft zwischen allen Punkten. bildet also die Ecken eines Tetraeders.
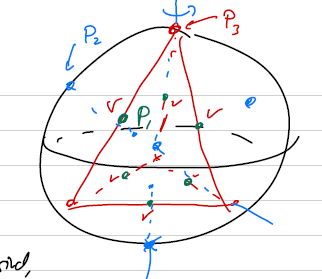
Stabilisatorgrößen 2-3-4
, wir können also wieder einen Punkt außer dem Punkt selbt und der Antipode finden und diesen um ein Viertel weiterdrehen. Wegen der willkürlichkeit des Punktes kann man ein Abstandsargument wie oben gebrauchen und bildet die Ecken eines Oktaeders.
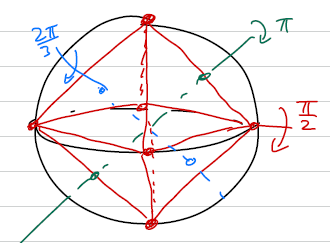
Stabilisatorgrößen 2-3-5
Durch Einsetzen in die Gleichung erhalten wir .
Wir wählen einen Punkt und führen eine Rotation um auf einen Punkt durch, der nicht oder ist. Dadurch haben wir nun Punkte.
Bei dieser Rotation muss man einen unkt entweder -mal rotieren um zum urspünglichen Punkt zurückzukommen oder der Punkt ist schon ein Fixpunkt.
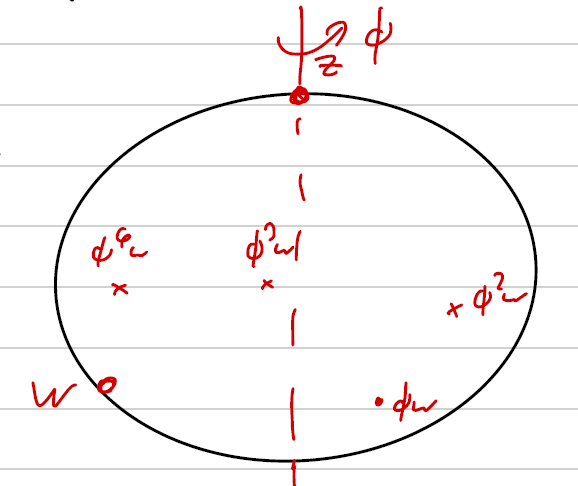Die Punkte von zerfallen also unter der Gruppe in kleinere Orbits , die die Größe oder haben müssen. Offensichtlich liegt noch ein Fixpunkt von in . Außerdem gibt es noch einen Punkt, auf der Kugel, den wir noch nicht bestimmt haben. Rotieren wir den, finden wir alle Punkte.
Betrachte im oberen Bild den Punkt . Rotieren wir diesen Punkt und argumentieren wie zuvor, muss auch der gegenüberliegende Punkt in liegen.
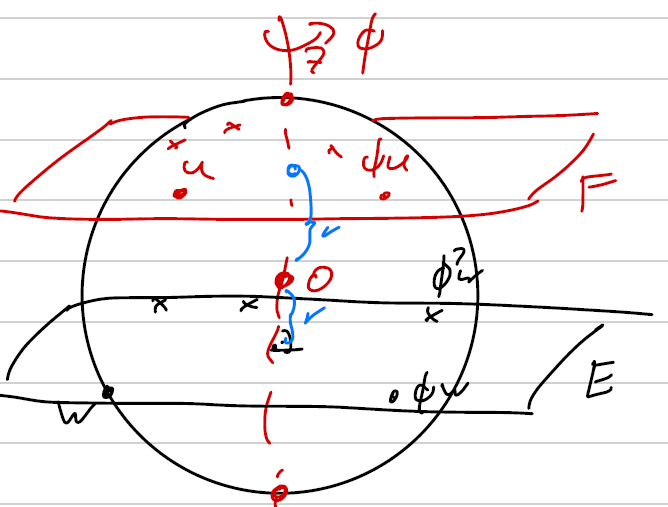Rotieren wir nun den Punkt um . Das sollten wir mal tun können, bevor wir wieder bei zurückkommen. Der Abstand von zu den Bildpunkten bleibt dabei immer gleich. Auf Ebene gibt es zwei Punkte mit Abstand . Auf Ebene gibt es maximal zwei Punkte, die auf dem Kreis liegen und den gleichen Abstand haben. Der letzte Punkt muss daher sein. Also ist der Abstand und damit bilden die Punkte die Ecken eines Icosaeders.