Alternierende Gruppe

Beschreibung

Die Alternierende Gruppe erhält man, indem man die Untergruppe aller Permutationen bildet, deren Signumsfunktion 1 ergibt.

Diese Gruppe ist wohldefiniert, da jedes Element invertierbar ist. (vgl. Umwandlung in Gruppe)

Charakterisierungen

Quadrierung einer Symmetrischen Gruppe

Nimmt man eine Symmetrische Gruppe $S_n$ und quadriert jedes Element darin, so so bilden die Ergebnisse $A_n$ eine Alternierende Gruppe

Erzeugendensystem

Die Menge aller $3$-Zykel auf $\{1,...,n\}$ bildet ein Erzeugendensystem von $A_n$

Eigenschaften

Ordnung

Die Ordnung einer Alternierenden Gruppe $A_n$ ist genau halb so groß wie die Ordnung einer Symmetrishcen Gruppe.

Normalteiler von $S_n$

Die Alternierende Gruppe $A_n$ ist ein Normalteiler der Symmetrische Gruppe $S_n$.

Die Signumsfunktion hat als Kern die Untergruppe $A_n$. Außerdem ist Signum für $n\ge 2$ surjektiv. Damit induziert sie nach Homomorphiesatz für Gruppen einen Isomorphismus $S_n/A_n\cong \{-1,1\}$

Dazu muss $A_n$ ein Normalteiler gewesen sein.

Beispiele

A3

$A_4$ beschreibt die Rotationssymmetrien eines gleichseitigen Dreiecks (glaube ich)

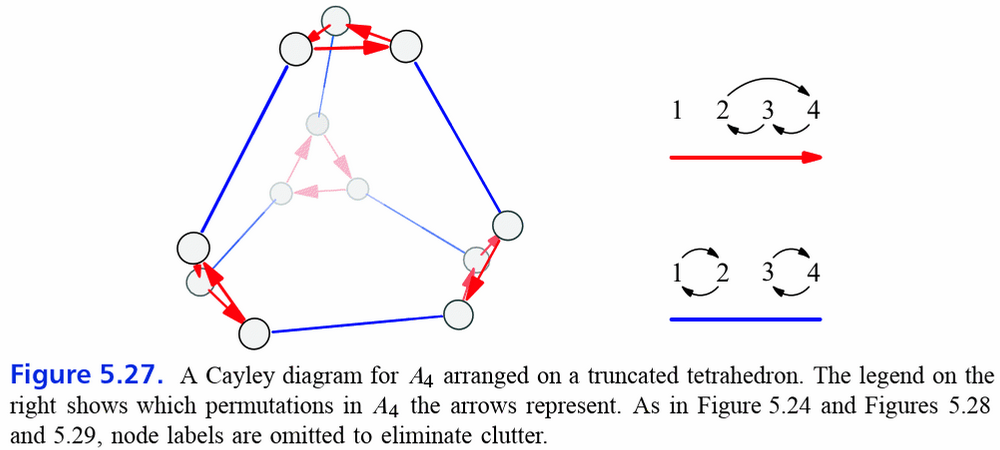
A4

$A_4$ beschreibt die Rotationssymmetrien eines Tetraeders

A5

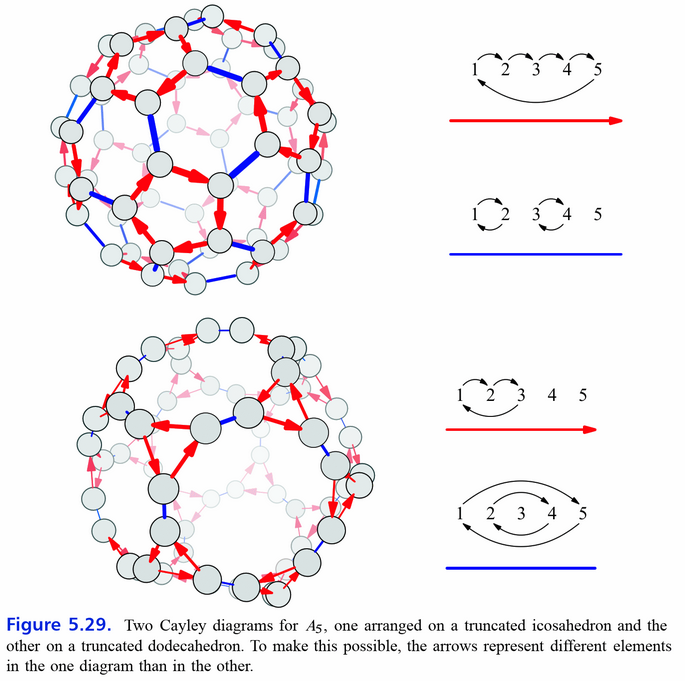
$A_5$ beschreibt die Rotationssymmetrien eines Dodekaeder und Ikosaeder