Cayley-Graph

Beschreibung

Eine Gruppe kann als eine Menge von Transformationen auf ein Objekt betrachtet werden. z.B. senkrechte und waagrechte Spiegelungen eines Rechtecks und ihre Verknüpfungen.

Um den Raum der Transformationen zu strukturieren, kann man ein Cayley-Diagramm (auch Cayley-Graph) nutzen. Zeichne dazu das gewöhnliche Rechteck. Zeichne nun neben das Rechteck das Bild einer horizontalen Spiegelung und zeichne zwischen die Rechecke einen Pfeil, der indiziert, dass das neue Rechteck durch eine horizontale Spiegelung erstellt werden kann.

Fügt man nun zu den zwei Rechtecken die Bilder einer vertikalen Spiegelung hinzu und zu diesen Bildern wieder die horizontale Spiegelung kann man beobachten, dass man durch die zwei Aktionen der Spiegelung von überall irgendwo hinkommt.

Das Resultat nach dem Zeichnen dieser Karte ist ein Graph mit Rechteckskonfigurationen als Knoten und den Generatoren als Kanten. Offensichtlich ist das Diagram von den gewählten Erzeugern abhängig.*

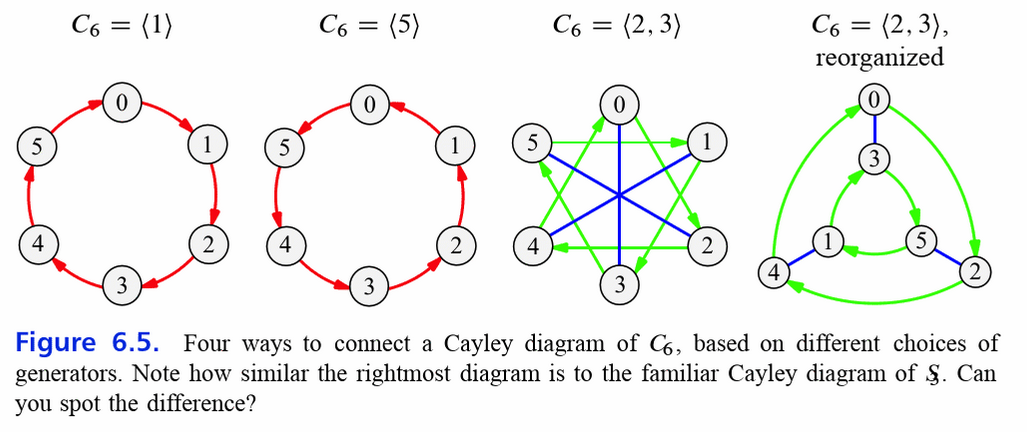
Jede Gruppe kann durch ein Cayley-Diagramm dargestellt werden.

Definition

Sei $G$ eine Gruppe und $S$ ein Erzeugendensystem von $G$. (o.E. ist das neutrale Element nicht darin enthalten). Der Cayley Grad ist ein gefärbter, Gerichteter Graph bezeichnet mit $\Gamma (G,S)$.

Für alle $g\in G$ und $s\in S$ besitzt der Graph $\Gamma (G,S,f)=(G,E)$ eine gefärbte Kante $(g,gs)\in E$ mit der Farbe $f:(g,gs)\mapsto s$ .

Eigenschaften

Gruppenelement induziert Graphautomorphismen

Jedes Element $g\in G$ der Gruppe induziert einen Graphautomorphismus, des Cayley-Graphen $\Gamma (G,S)$.

Definiere den Automorphismus mit ${\varphi }_g(v)=v$.

Graphenknoten werden damit nämlich bijektiv auf andere Knoten abgebildet. Eine Kante $(h,hs)$ wird auf $(hg,ghs)$ also auf eine Kante gleicher Farbe abgebildet. Diese Kante war vorher schon da war. Umgekehrt hat auch jede Bildkante ein Urbild. Damit erhält ${\varphi }_g$ die Struktur von Knoten, Kanten und Farben, ist also ein Graphautomorphismus.

Isomorphie $G\cong Aut(\Gamma (G,S))$

Die Gruppe $G$ ist isomorph zur Graphautomorphismengruppe von $\Gamma (G,S)$. Wir kürzen ab $\Gamma (G,S)=\Gamma$

Beweis: Aus oberer Eigenschaft, dass jedes $g\in G$ einen Automorphismus induziert erhalten wir leicht einen Homomorphismus $\Phi :G\to Aut(\Gamma ),g\mapsto {\varphi }_g$. Dieser ist injektiv, denn jedes ${\varphi }_g$ bildet $e$ auf $g$ ab, ist also verschieden.

Zeige nun Surjektivität. Sei $\varphi \in Aut(\Gamma )$. Dieser bildet den neutralen Knoten auf $g$ ab, d.h. $\varphi (1)=g$. Behauptung: $\varphi (v)={\varphi }_g(v)$. Nutze vollständige Induktion über der Wortlänge von $v$, d.h. die kürzeste Schreibweise von $v$ als Produkt der Erzeuger $S$ und ihrer Inversen.

Das einzige Element $v\in G$ mit Wörtlänge von $0$ ist $1$. Wegen $\varphi (1)=g={\varphi }_g(1)$ ist die Gleichung ist also für alle $v$ mit Länge $0$ erfüllt. Nehme an, die Gleichung $\varphi (v)={\varphi }_g(v)$ gilt für $v$ mit Wortlänge $n$. Zeige Gleichung für Wortlänge $n+1$: Nehme an $v$ hat Länge $n+1$. Dann gibt es ein $w\in G$ mit Länge $n$ und $s\in S\cup S^{-1}$, sodass $v=ws$. Nach IV gilt $\varphi (w)={\varphi }_g(w)$. Da $\varphi$ und ${\varphi }_g$ beides Graphautomorphismen sind kommt man durch das Folgen der Kante $s$ zum gleichen Wert. Also gilt $\varphi (v)={\varphi }_g(v)$.

Es gibt also zu jeder Gruppe immer ein Geometrisches Objekt, dessen Symmetriegruppe, isomorph zur Gruppe ist.

lit_carterVisualGroupTheory2021 lit_clayOfficeHoursGeometric2017