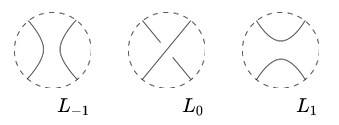Khovanov-Homologie

Beschreibung

Die Khovanov-Homologie ist eine Knoteninvariante. Es ordnet einer Verschlingung einen Kettenkomplex zu und ist zudem einer Verallgemeinerung des Jones-Polynom. Es mag erstmal ungewöhnlich erscheinen, wie ein Kettenkomplex als Objekt betrachtet werden kann. Das ist ganz einfachmöglich, indem die n-Ketten in einem Graduierter Vektorraum zusammengefasst werden.

Berechnet wird es genau so wie das Jones-Polynom durch eine induktive Betrachtung von Reguläre Projektion (Knoten).

Definition

Sei $L$ ein Diagramm einer Verschlingung. Die Khovanov-Klammer $[L]$ wird durch folgende Eigenschaften eindeutig festgelegt

• Die Khovanov-Klammer der leeren Menge ist der Komplex $0\to \mathbb{Z}\to 0$
• $[◯\bigsqcup L]=V\otimes [L]$
• Wenn Diagramme dreier Verschlungen $L_{-1},L_0,L_1$ sich folgendermaßen unterscheiden, dann ist $[L_0]=\mathcal{F}(0\to [L_1]\stackrel{d}{\to }[L_{-1}]\{1\}\to 0)$

Dabei ist $V$ der Gradierter Vektorraum mit Erzeugern $q,q^{-1}$ in Graden $1$ und $-1$. $\{1\}$ ist der Gradshift des Graduierter Vektorraum um $1$ und $\mathcal{F}$ macht aus einem Doppelkomplex einen Komplex durch Bilden direkter Summen entlang Diagonalen.

Eigenschaften

Graduierte Euler-Charakteristik

Die Graduierte Euler-Charakteristik ist das nicht-normalisierte Jones-Polynom von $L$ ${\chi }_q([L][-n_{-}]\{n_{+}-2n_{-}\})$ wobei $n_{-}$ die Anzahl an links-orientierten Übergängen der Verschlingungsprojektion ist und $n_{+}$ die Anzahl der positiven.

lit_bar-natanKhovanovCategorificationJones2002 lit_bar-natanKhovanovCategorificationJones2002