Konferenz Hamada - Exotic 4-manifolds with signature zero via Lefschetz fibrations

Abstract

We will talk about the construction of our new examples of simply-connected closed exotic 4-manifolds with signature zero. Notably, we will present the smallest examples known to date. Our method employs the time-honored approach of reverse-engineering, while the key new ingredients are the model manifolds that we build as Lefschetz fibrations. A detailed discussion on their monodromy factorizations will be presented.

1. Main Result

Theorem 1 (Baykur)

For every $k\ge 5$ and for every $l\ge 4$, there are infinitely many, pairwise non-diffeomorphic, symplectic $4$-mfd that are homeomorphic to ${\#}^{2k+1}(S^2\times S^2),$ and ${\#}^{2l+1}(\mathbb{C}{P}^2\#\mathbb{C}{P}^2)$ respectively.

2. Background

Definition Standard Manifold

“standard” sim-conn $C^{\infty }$ $4$-mfd are defined as Connected sums of $S^4,C{P}^2,S^2\times S^2,K3,\overline{K3}$.

Their Homeo-Types are exhausted by $\{\begin{array}{ll}m(S^2\times S^2)\#nK3& \text{spin }\sigma =-16n\\ mC{P}^2\#n{\overline{CP}}^2& \text{non-spin}\sigma =m-n\end{array}$ and in particular for $\sigma =0$ $\{\begin{array}{ll}n(S^2\times S^2)& \text{spin}\\ n(C{P}^2\#{\overline{CP}}^2)& \text{non-spin}\end{array}$

Are there any exotics structures? Yes, e.g. $C{P}^2\#n{\overline{CP}}^2$ for $n\ge 2$ and $K3$. Open: $S^4,nC{P}^2,n(S^2\times S^2),n(C{P}^2\#{\overline{CP}}^2)$.

Symplectic geography

Definition

Let $\sigma$ denote the sign and $e$ the Euler characteistic.

• $K^2=C_1^2=3\sigma +2e$
• ${\chi }_h:=\frac{c_1^2+c_2}{12}=\frac{\sigma +e}{4}$ ist the holomorphic euler characteristic.

Geography Problem

Dertermine $(x,y)\in {\mathbb{N}}_0\times {\mathbb{N}}_0$ for which there exists a closed simple-connected minimal symplectic $4$-mfd $X$ of general type with $x={\chi }_h,y=K^2$.

When $\sigma =0$, the only possible homeo types are $\{\begin{array}{l}m(S^2\times S^2)\\ n(C{P}^2\#{\overline{CP}}^{2)}\end{array}\stackrel{\text{almost complex}}{⟹}\{\begin{array}{l}{\#}^{2k+1}(S^2\times S^2)\\ {\#}^{2l+1}(C{P}^2\#{\overline{CP}}^2)\end{array}$

Depending on the values of ${\chi }_h$ and $K^2$ the Geography Problem has been solved for the following manifolds:

We now take a look at model manifolds. Previous results state that algebric sufaces with $\sigma \ge 0$ and non-trivial fundamental group turn into manifolds with ${\pi }_1=1,\sigma =0$ after applying Luttinger surgery and blow-ups.

Our method: Turns a Lefschetz fibration (+trivial extension) with $\sigma =0$ and nontrivial fundamental group into manifolds with ${\pi }_1=1,\sigma =0$ after applying Luttinger surgery. The idea is to extend the yellow fibration by a trivial extension first.

3. Lefschetz Fibration

Theorem

Let $g\ge 2$ and $f:X^4\to {\Sigma }_n$ be a Lefschetz fibration Then $X$ admits a symplectic structure.

It can be described as follows: 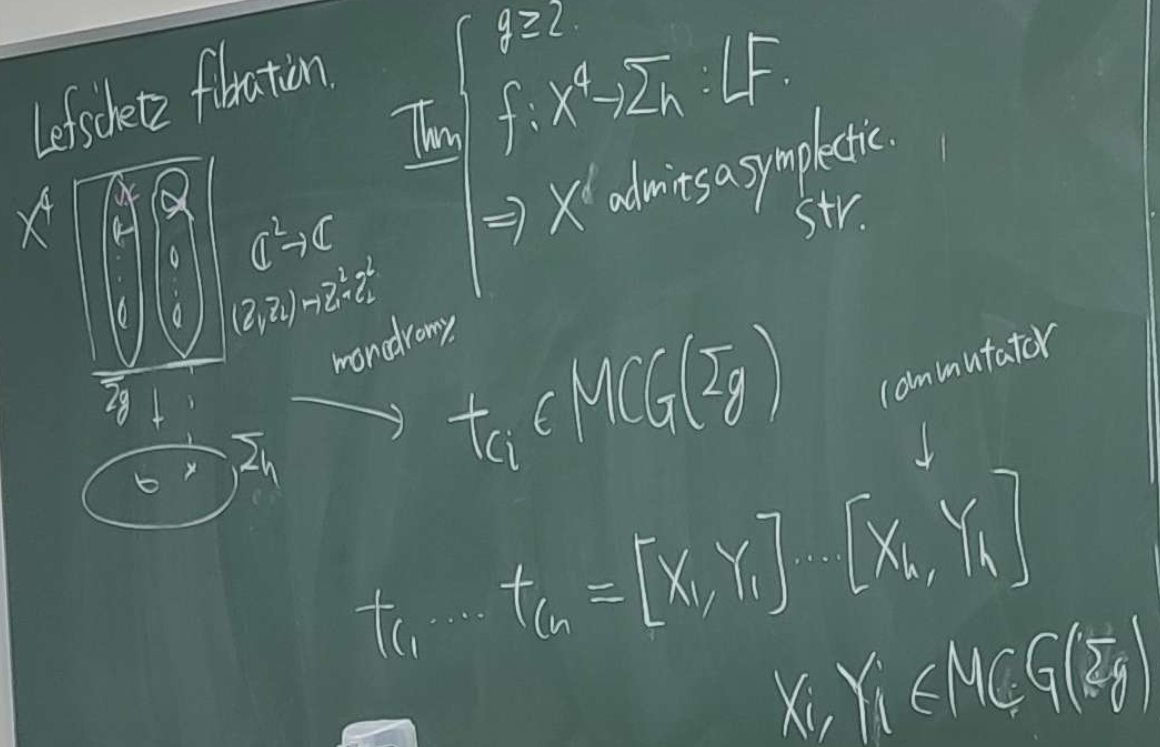In our case, the kernels are

• Lefschetz Fibrations with $\sigma =0,g=9,h=0$ and $n=48$ critical points, spin
• Lefschetz Fibrations with $\sigma =0,g=4,h=1$ and $n=4$ critical points, non-spin
• Lefschetz Fibrations with $\sigma =0,g=5,h=1$ and $n=4$ critical points, spin

Our technique to construct $LF/T^2$ is the following. We start with a cylinder with a hole, glue the ends together and apply Dehn Twists to get a description of the commutator $[X,Y]$

4. Signature Zero Relations

The author describes a few manifolds with zero relations that he knows. For $g=1$, the examples can be taken from the following pictures.

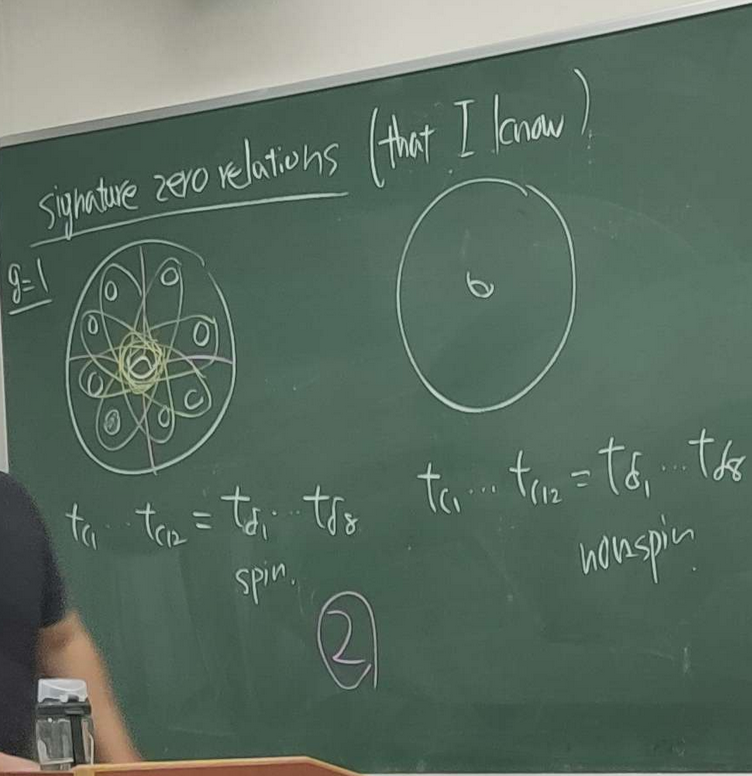
For $g=2$ we have the following examples:

• BK LF (LP) with $n=7,k=\#\partial \text{Components}=3$
• Matsumoto LF (LP) $n=8,k=4$ spin non-spin

For $g=3$ we have the Smith LP $n=12,k=4$ with spin