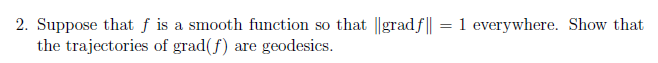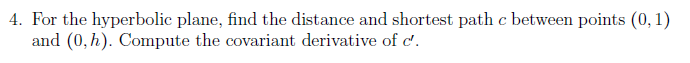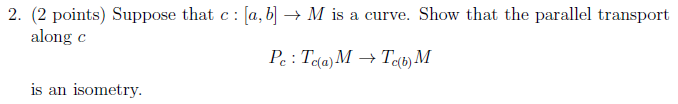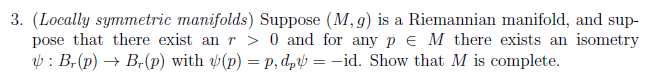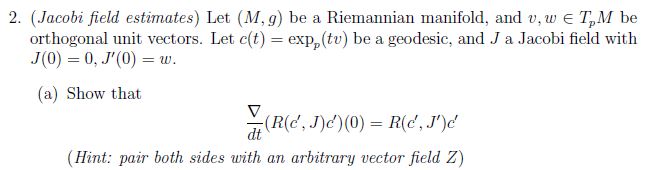Beschreibung
Das soll ein ähnliches Konzept wie bei Stochastik sein. Ich fasse alle Themen der Vorlesung zusammen, um Klausuraufgaben zu antizipieren. Das Vorgehen ist wie bei Stochastik, dort hat es ja ganz gut geklappt, wie ich an der Klausur erkannt habe.
Ich bin gerade durch einige Übungen durchgegangen. Mir ist aufgefallen, dass viele echt keine gute Klausuraufgaben ergeben. Oft braucht man eine sehr spezielle Idee oder die Aufgabe ist einfach viel zu schwer. Eventuell sollte ich mir selbst Übungsaufgaben ausdenken oder mal in die Bib schauen.
Ich sollte außerdem die Probeklausur analysieren. Vielleicht gelingt es mir, einige Aufgaben zu verallgemeinern. Ich weiß zum Beispiel, dass er Berechnungen hasst. Er wird demnach sicher keine stellen.
In der VL gibt es viele Formeln, und Gleichungen die man kennen muss. Ich erstelle mir Karteikarten dafür.
Themen
Riemannsche Mannigfaltigkeit, Metrik und Zusammenhang (4/11)
Zu Beginn werden Riemannsche Mannigfaltigkeit, unser primäres Ziel zum Studieren definiert. Hierfür benötigen wir eine Riemannsche Metrik oder ein Levi-Cevita-Zusammenhang. Die beiden Sachen stehen durch die Koszul-Formel in Verbindung.
Example
Example
Example
Example
Example
Example
- Sei eine Riemannsche Mannigfaltigkeit. Zeige, dass die Pfadmetrik die Topologie der Mannigfaltigkeit induziert
Gradient und Hessesche (4/11)
Wir definieren eine reellwertige Funktion auf einer Mannigfaltigkeit. Dank der Riemannschen Metrik können wir nun den Gradienten und die Hessesche verallgemeinern.
Example
Example
Example
- Berechne die Krümmung des Hyperboloids und der Hyperbolischen Halbebene.
Example
- Zeige, dass für keine Hyperflächen existieren, die negative Schnittkrümmung besitzen
Hyperbolische Geometrie (3/11)
Die Hyperbolische Halbebene ist ein Beispiel einer Mannigfaltigkeit. Wie wir später lernten, ist sie die eindeutige vollständige, einfach zusammenhängende Mannigfaltigkeit mit konstanter Krümmung . Wir klassifizierten Isometrien der Hyperbolischen Geometrie als Möbiustransformationen.
Example
- Hier konnte man einfach das Kurvenintegral hinschreiben und feststellen, dass eine Projektion an die -Achse die Kurve immer kürzt. Wie man den Zusammenhang berechnet, weiß ich allerdings nicht
Isometrien (4/11)
Wir definierten Isometrien als Funktionen, die die Riemannsche Metrik erhalten. Isometrien tauchen die ganze Zeit auf. Ich muss mal schauen, ob wir jemals eine Aufgabe spezifisch dazu hatten.
Example
Example
Example
- Sei eine lokale Isometrie zwischen Mannigfaltigkeiten . Zeige, dass
Geodätische & Exponential (6/11)
Wir definierten Geodätische als die Kurven, ohne Krümmung. Wir stellten fest, dass längenminimierende Kurven Geodätische sind und dass in total normalen Umgebungen um einen Punkt immer eine eindeutige längenminimierende Kurve zu existiert. In total normalen Umgebung ist des weiteren das Exponential (Geodätische) ein Diffeomorphismus. Ich lernte das Gausssches Lemma, das besagt, dass Geodätische immer senkrecht aus Kugeln austreten.
Example
Example
Nord-Süd-Dynamik & Ping-Pong (4/11)
Wir lassen eine Gruppe durch Translation entlang zweier Geodätischer auf der Poincaré Scheibe wirken. Anhand der Nord-Süd-Dynamik sind die Bedingungen des Ping-Pong Lemma erfüllt, d.h. die Gruppe ist frei durch die Translationen erzeugt.
Da dies nie in Übungen behandelt wurde, ist es wahrscheinlich nicht so wichtig.
Krümmungen (5/11)
Wie führten viele verschiedene Definitionen von Krümmungen ein.
Example
Zeige, dass 1-dimensionale Mannigfaltigkeiten immer Krümmung haben.
Example
Example
Example
- Seien total geodätische Untermannigfaltigkeiten. Zeige, dass eine total geodätische Untermannigfaltigkeit von ist.
Jacobi-Felder (6/11)
Von großer Bedeutung ist hierbei das Jacobi-Feld, das das Entwicklungsverhalten naheliegender Geodätischen beschreibt. Es gibt damit eine wichtige Charakterisierung von positiver Krümmung in Räumen.
Example
Variationen der Energie (7/11)
Wir weisen einer Kurve eine Energie (Kurven) zu. Kurven mit (lokal) minimierender Energie sind hierbei Geodätische. Indem wir zeigen, dass eine Kurve durch Verschiebung entlang eines Vektorfeldes an Energie verliert, lässt sich zeigen, dass die Ursprungskurve keine Geodätische war.
Konjugierte Punkte (6/11)
Verlassen zwei naheliegende Geodätischen einen Punkt und treffen irgendwann wieder aufeinander, so bezeichnen wir den Schnittpunkt als Konjugierter Punkt. Spätestens ab diesem Punkt hören Geodätische auf, längenminimierend zu sein. Sie hören des weiteren auf längenminimierend zu sein, wenn zwei es Geodätische zu dem Punkt gibt.
Vergleichssätze (5/11)
Haben wir eine Mannigfaltigkeit die überall negativer gekrümmt ist als eine Modellmannigfaltigkeit, können wir spezielle Aussagen über das Verhalten der Jacobi-Felder treffen. Der wichtigste Satz ist der Vergleichssatz von Rauch aber es gibt auch Längenvergleich, Dreiecksvergleiche und dazu bezogen Vergleichsscharnier.
Aus dem dritten Dreiecksvergleich ergibt sich eine metrische Charakterisierung von Krümmung. Dies ergibt die Definition des CAT(k) Raum.
- Bei der Aufgabe gibt es zwei Lösungen. Entweder man berechnet den Ball durch eine Substitution, einen Cavalieri und

Transvektionen & Killing Felder (0/11)
Ich habe keine Ahnung, was ein Killing Feld ist. Das muss ich mir dringend noch ansehen..
Sonstiges
Hier stecke ich alle Themen rein, die mal angesprochen wurden, von denen ich aber nicht ausgehe, dass sie klausurrelevant sind. (Da es viele bessere Alternativen gibt).
Klausur
Aufgabe 1
Die Aufgabe 1 habe ich sehr gut gelöst, ich sage mal nichts mehr dazu.
Aufgabe 2
Die Idee bei Aufgabe a) war zu zeigen, dass der Zusammenhang alle Voraussetzungen eines Levi-Cevita-Zusammenhangs erfüllt. Das wäre eigentlich eine typische Klausuraufgabe gewesen. Wenn ich das mindestens einmal geübt hätte, wäre das Vorgehen offensichtlich gewesen. Für das nächste mal sollte ich einfach mehr alte Übungsblätter machen. Die älteren geraten nämlich schneller in Vergessenheit.
Bei b) habe ich einfach den letzten Satz nicht gelesen. Es wäre sehr empfehlenswert, nach jeder Aufgabe mit einem Stift durch die Aufgabenstellung zu gehen und alles zu markieren, was ich bereits gemacht habe.
Was das Problem bei der c) war, habe ich noch nicht ganz verstanden. Irgendetwas damit, dass die Ableitung einer Ableitung nicht notwendigerweise 0 sein muss, wie aus b) folgernd.
Ich gebe mir 4/12 Leichtsinnsfehlerberichtigte Punkte
Aufgabe 3
Bei der Aufgabe 3 a) habe ich die Aussage nicht für alle Kurven gezeigt. Ich habe nicht verstanden, dass die Geodätischen nicht notwendigerweise durch verlaufen müssen. Hätte ich das gesehen, hätte ich vielleicht Punkte mehr bekommen. Vielleicht hätte mir hier ein Bild weitergeholfen? Am Bild hätte ich Spezialfälle erarbeiten können. Als nächsten Schritt hätte es Vergleichsgeometrie gebraucht. Eigentlich hätte mir auch auffallen sollen, dass Vergleichsgeometrie nie abgefragt wurde, obwohl es Teil des Stoffs war. Ich gebe mir die beiden Punkte mal nicht, da ich nicht weiß, ob ich darauf gekommen wäre. Das Problem ist, dass ich zu abhängig von Schlüsselwörtern bin. Ich erwarte nicht, dass Klausuren aus mehreren Schritten bestehen können. Ich sollte die Beweis zumindest im Kopf so strukturieren, dass ich auch nach Schlüsselwörtern in meinem eigenen Beweis Ausschau halten kann.
Das macht also 6/8 Punkte
Aufgabe 4
Ich sollte hier bei a) auch die Rückrichtung zeigen. Das habe ich einfach vergessen. Ich muss die Aufgabenstellungen unbedingt markieren. Aufgabe b) war einfach zu kompliziert. Nachdem ich aber sehr, sehr wenig für eine Aufgabe mit 6 Punkten geschrieben habe, hätte mir etwas auffallen sollen.
Ich gebe mir 6/10 Leichtsinnfehlerberichtigten Punkten
Ergebnis
Ohne Leichtsinnsfehler hätte ich locker 4,5 Punkte mehr bekommen können. Das hätte sogar für die Note 2.3 gereicht. Sonst waren die Aufgaben einfach sehr schwer. Eventuell hätten nur mehr Übungsaufgaben weitergeholfen. Eine 1 wäre wirklich schwierig gewesen.