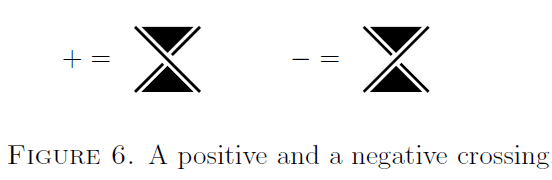Thompsons Gruppe F

Beschreibung

Thompsons Gruppe $F$ ist eine Endlich Erzeugte Gruppe mit einigen interessanten Eigenschaften. Sie ist eigentlich Teil von mehreren Gruppen, die Thompson konstruiert hat.

Definition: Intuitive Präsentation

Thompsons Gruppe $F$ ist definiert als $F:=⟨x_0,x_1,...\mid \{x_k^{-1}{x}_n{x}_k=x_{n+1}:k,n\in \mathbb{N},k<n\}⟩$

Das Konjugieren eines Gruppenelements mit einem niedrigerem gibt dem Element quasi ein Upgrade.

Definition: Endliche Präsentation

Die Gruppe ist Endlich Erzeugte Gruppe, denn man kann folgende Präsentation wählen: $F\cong ⟨a,b\mid [a{b}^{-1},a{b}^{-1}a],[a{b}^{-1},a^{-2}b{a}^{-2}]⟩$ wobei $[a,b]$ der Kommutator von $a$ und $b$ ist.

Definition: Gruppe von Homöomorphismen

Thompsons Gruppe F ist die Gruppe aller Stückweise linearer Homöomorphismus des Einheitssegments, denen folgende zwei Einschränkungen unterliegen:

• Es gibt nur endlich viele Bruchstellen, welche an Punkten der Form $(\frac{k}{2^n},\frac{l}{2^m})$
• Alle Steigungen sind eine Potenz von $2$.

Definition: Gruppe von Doppelbäumen $(T_{+},T_{-})$ (doppelt, weil sie an den Blättern zusammengesteckt sind). Bäume sind äquivalent, wenn sie durch das Entfernen von Rauten ineinander überführt werden können. Das Produkt ist gegeben durch: $(T_{+},T)\cdot (T,T_{-})=(T_{+},T_{-})$ Das triviale Element ist durch jedes Paar $(T,T)$ gegeben.

Der Zusammenhang zwischen den Bäumen und den Homöomorphismen ist sehr interessant. Wir betrachten Zahlen aus $\mathbb{Z}\left[\frac{1}{2}\right]$ und betrachten sie in Binärschreibweise. Wir werfen die Zahl in den oberen Baum. Je nachdem, ob eine $0$ oder $1$ kommt, geht die Zahl nach links oder rechts und die Stelle wird entfernt. Ist sie bei der mitte angekommen, werden $0$ und $1$ wieder hinzugefügt, abhängig davon, ob die Zahl von links oder rechts kommt. Offensichtlich ist damit beispielsweise $(T,T)$ die Identität.

Satz: Charakterisierung der Abelianisierung

Die Abelianisierung ist isomorph zur Gruppe $F/[F,F]=\mathbb{Z}\times \mathbb{Z}$ und kann beschrieben werden durch $\pi (f)=({\log }_2{f}^{\prime }(0),{\log }_2{f}^{\prime }(1))$

Eigenschaften

Satz: Ungewöhnliche Eigenschaften

Die Thompson Gruppe $F$ hat einige interessante Eigenschaften, die widersprüchlich klingen.

• $F$ ist endlich präsentiert und hat $F\times F$ als Untergruppe
• $F$ ist endlich präsentiert und ist eine HNN-Erweiterung von sich selbst
• $F$ hat exponentielles Wachstum aber enthält keine Freie Gruppe von Rang 2.

Satz: Torsionsfreiheit

$F$ ist eine Torsionsfreie Gruppe, wie man durch Potenzierung der Stückweise linearer Homöomorphismus des Einheitssegments sehen kann.

Satz: Normalform

Jedes Element $g$ in $F$ kann geschrieben werden als $x_0^{a_0}...x_n^{a_n}{x}_n^{-b_n}...x_0^{-b_0}$ mit $a_0,...,a_n,b_0,...b_n\in {\mathbb{N}}_0$. Entweder $a_n$ oder $b_n$ ist $0$, und wenn $a_i\ne 0$ und $b_i\ne 0$ dann ist auch $a_{i+1}\ne 0$ und $b_{i+1}\ne 0$.

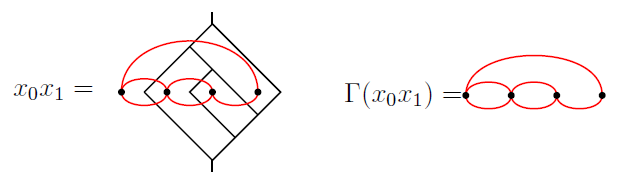
Satz: Zusammenhang zu Knoten und Verschlingungen

Die Elemente von $F$ stehen in Zusammenhang mit Knoten und Verschlingungen. Die Idee ist aus den Bäumen ein Diagramm einer Verschlingung zu erstellen.

1. Beginne mit einem Doppelbaum $(T_{+},T_{-})$
2. Bilde ein Tait-Diagramm, indem in der oberen Halbeebene eine Kante durch jedes steigende Segment und in der unteren Halbebene eine Kante durch jedes fallende Segment gezeichnet wird.
3. Zeichne den Medialgraphen. Dieser hat überall Valenz $4$
4. Mache die oberen Knoten zu positiven Kreuzungen und die unteren zu negativen

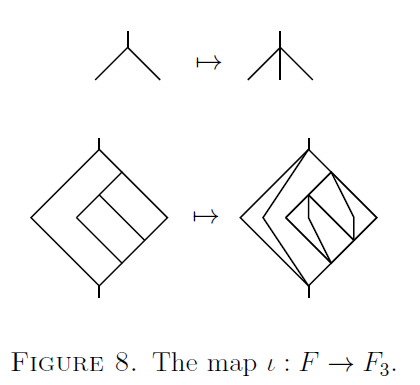
Satz: Zusammenhang zu Knoten und Verschlingungen 2

Die Elemente von $F$ stehen in Zusammenhang mit Knoten und Verschlingungen. Die Idee ist aus den Bäumen ein Diagramm einer Verschlingung zu erstellen.

1. Beginne mit einem Doppelbaum $(T_{+},T_{-})$
2. Mache einen Doppeltrinärbaum daraus, indem eine dritte Kante zwischen links und rechts eingefügt wird.
3. Verbinde die obere und untere Kante
4. Die Knoten zu Mistgabeln

Die obere Herangehensweise gibt uns tatsächlich eine Methode aus jedem Element von $F_3$ eine Verschlingung zu erstellen.