Jacobi-Feld

Beschreibung

Das Jacobi-Feld ist ein Vektorfeld (Vektorraum) auf einer Riemannsche Mannigfaltigkeit, die beschreibt, wie sich Geodätische ausbreiten. Es handelt sich um einen Spezialfall eines Variationsfeld.

Definition

Einführendes Beispiel

Sei ${\gamma }_t$ eine glatte Ein-parameter Familie von Geodätischen. Dann ist $J(t)=\frac{\partial {\gamma }_s(t)}{\partial s}{|}_{t=0}$ Da ${\gamma }_t$ eine Familie von Geodätischen ist, sind die Möglichkeiten bereits sehr beschränkt. Angenommen, die Geraden beginnen in der Umgebung eines Punktes parallel. Dann ist is möglich, die Entwicklung der Geodätischen zu untersuchen. Wir stellen fest, dass bei positiver Krümmung die Geodätischen zusammenlaufen, während sie bei negativer Krümmung auseinanderlaufen.

Tatsächliche Definition

Das Jacobi-Feld wird definiert in Krümmung eines Zusammenhangs. Kompakt ist es ein Feld, dass die Jacobi-Gleichung erfüllt: $\ddot{J}-R(\dot{c},J)\dot{c}=0$ Das $R(\dot{c},J)$ ist dabei die Krümmung eines Zusammenhangs

Intuition

Angenommen wir befinden uns im ${\mathbb{R}}^2$ mit einem beliebigen Levi-Cevita-Zusammenhang. Wir wollen untersuchen, wie sich Geodätische in diesem Ram krümmen. Unsere anfängliche Geodätische $c$ beginnt im Punkt $0$ und läuft dann euklidisch gerade nach rechts. Rotieren wir den Austrittswinkel ein wenig in positiver Drehrichtung, so erhalten wir eine neue (möglicherweise euklidisch gekrümmte) Geodätische $c^{\prime }$. Die Vektoren, die die Punkte der ursprünglichen Geodätischen mit der neuen verbinden bilden bei kleinen Rotationen das Jacobi-Feld. 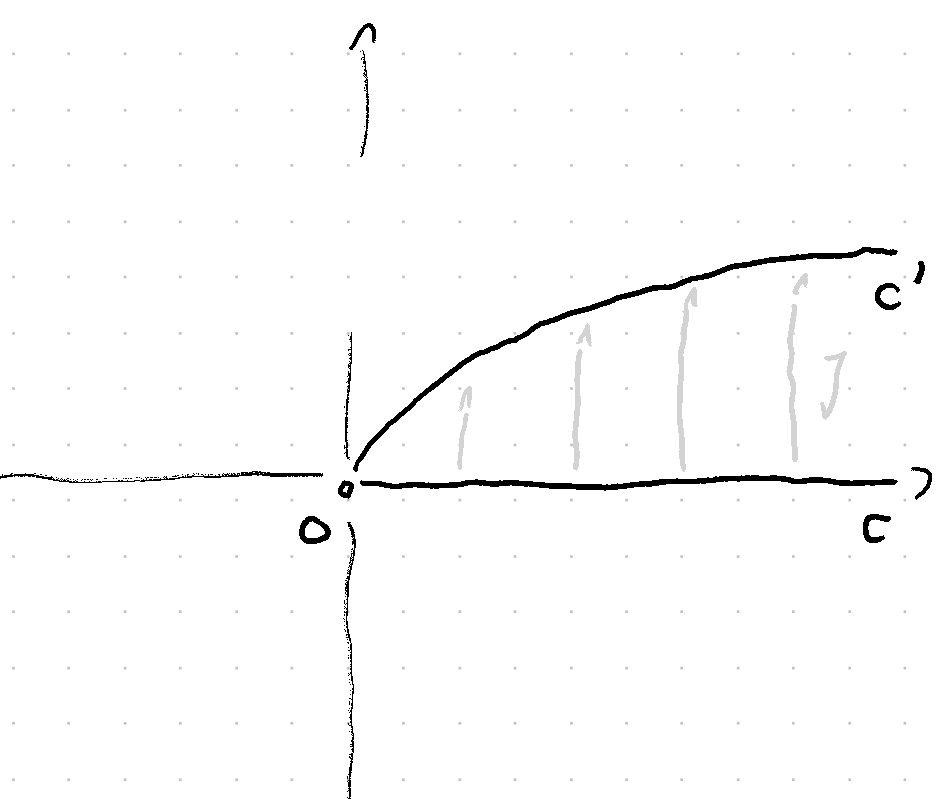Wir nehmen nun die vereinfachende Annahme an, dass das Jacobi-Feld ausschließlich aus einer Senkrecht-Komponente besteht. Das Jacobi-Feld sieht somit aus wie ein Funktionsgraph. Dessen Steigung in jedem Punkt gibt den Wert $\dot{J}$ an. Dessen Krümmung gibt den Wert $\ddot{J}$ an. Wir beobachten, dass der Abstand zwischen $c$ und $c^{\prime }$ kleiner wird, wenn $\ddot{J}$ negativ ist und größer wird wenn $\ddot{J}$ positiv ist.

Wir erhalten dadurch eine fantastische Intuition für den Wert $R(\dot{c},J)\dot{c}$. Das ist nämlich die Richtung, in die sich eine Geodätische krümmen wird, wenn wir sie in Richtung $J$ verschieben.

Eigenschaften

Eindeutigkeit

Sei $c:[a,b]\to M$ eine Lokale Geodätische (Mannigfaltigkeit) und $v,w\in T_{c(0)}M$ existiert eine eindeutiges Jacobi Feld $J$ entlang $c$ mit $J(0)=v,\dot{J}(0)=w$.

Beweis: Wähle parallele orthonormale Vektorfelder $b_i:[a,b]\to TM$ entlang $c$. Jedes Vektorfeld entlang $c$ kann dann mit dieser Basis geschrieben werden: $J(t)=\sum f^i{b}_i(t)$. Zweifaches kovariantes Differenzieren ergibt wegen Parallelität $\ddot{J}(t)=\sum {\ddot{f}}^i{b}_i(t)$ Nun lässt sich die Gleichung $\ddot{J}-R(c^{\prime },J)c^{\prime }=0$ als Lineare Differentialgleichung verstehen. Diese hat eine eindeutige Lösung.

Jacobi-Feld berechnet die Ableitung der Exponentialfunktion (Wichtig!)

Sei $c(t)={\exp }_{p}tv$ eine Geodätische und $J$ ein Jacobi Feld entlang $c$ mit $J(0)=0$. Sei $w=\dot{J}(0)$ und sei $v(s)$ eine Kurve mit $v(0)=v,v^{\prime }(0)=w$. Dann gilt $J(t)=\frac{\partial }{\partial s}{\exp }_{p}tv(s)=d_{tv}{\exp }_{p}tw$ Für einen Exponential (Geodätische), für die $1$ definiert ist gilt somit $d_v{\exp }_{p}w=J(1)$ Eine weitere Folgerung ist zudem, dass Isometrische Einbettungen $\varphi :M\to N$ Jacobi-Felder auf Jacobi-Felder abbildet.

Die Bedingung $J(0)=0,\dot{J}(0)=w$ hat eine wichtige Bedeutung. Richten wir $c(t)$ so aus, dass es nach rechts zeigt, so beschreibt $w$ die Austrittsrichtung der Geodätische $c^{\prime }$ aus der oben stehenden Intuition. Bewegen wir die Austrittsrichtung von $c$ in Richtung $w$, so bewegt sich auch die Geodätische festgelegt durch das Exponential. Wir definieren hier also eine Variation von Vektorfeldern. Dass dies ein Jacobi-Feld impliziert ist klar. Des weiteren erfüllt das Feld die Anfangsbedingungen.

Abschätzung des Jacobi-Feldes

Sei $(M,g)$ eine Riemannsche Mannigfaltigkeit und $v,w\in T_{p}M$ orthonormale Vektoren. Sei $c(t)={\exp }_p(tv)$ eine Lokale Geodätische (Mannigfaltigkeit) und $J$ ein Jacobi-Feld mit $J(0)=0,J^{\prime }(0)=w$. Dann gilt die Abschätzung: $\Vert J(t)\Vert =t-\frac{1}{6}g(R(v,w)w,v)t^3+o(t)$

Beispiele

Jacobi Feld mit Änderung entlang der Kurve

Sei $J(0)=0,\dot{J}(0)=b\cdot c^{\prime }(0)$ entlang $c$ mit Einheitsgeschwindigkeit. Dann ist $J(t)=d_v{\exp }_{p}t{c}^{\prime }(0)$ ein Jacobi-Feld