Beschreibung
Eine Funktionenfolge heißt gleichmäßig konvergent, wenn die Geschwindigkeit mit der die Funktion punktweise gegen einen Grenzwert konvergiert nicht vom Funktionswert abhängt.
Das ist gegeben, wenn man die Funktion durch eine Funktionenfolge abschätzen kann, die überall gleich ist.
Definition
Die Folge konvergiert genau dann gleichmäßg gegen , wenn Das ist genau dann gegeben, wenn
Eigenschaften
Beispiel
Punktweise aber keine gleichmäßge Konvergenz
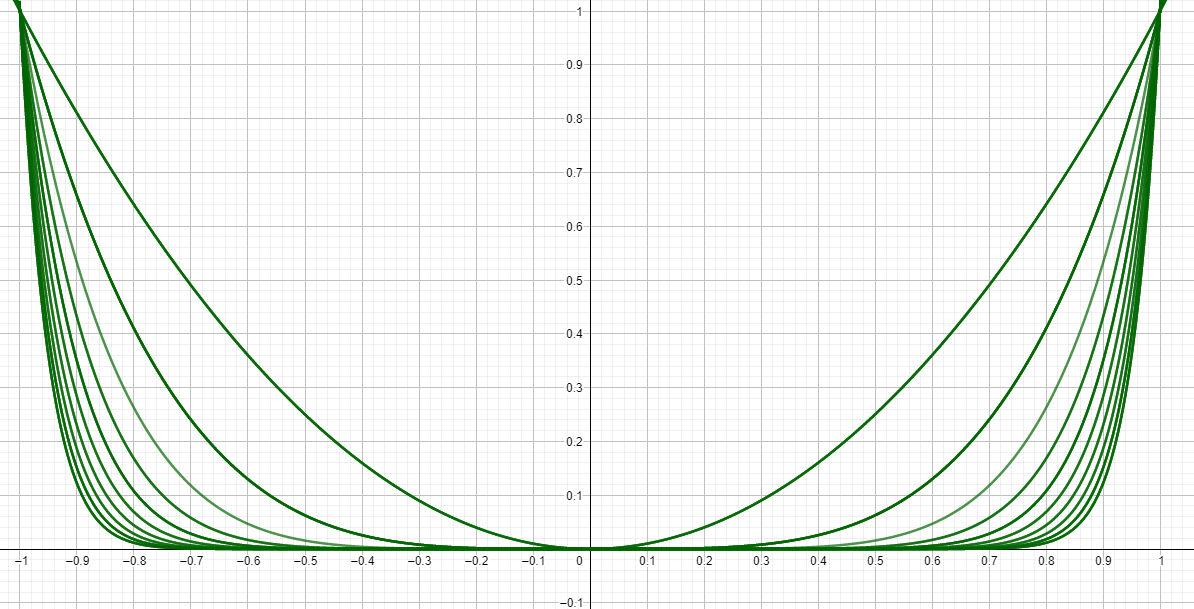 Die Funktionenfolge konvergiert punktweise gegen eine Funktion, die überall ist außer bei , wo sie ist. Das Supremum oben konvergiert nicht gleichmäßig gegen . Da es in einer Umgebung um immer ein gibt, bei dem .
Die Funktionenfolge konvergiert punktweise gegen eine Funktion, die überall ist außer bei , wo sie ist. Das Supremum oben konvergiert nicht gleichmäßig gegen . Da es in einer Umgebung um immer ein gibt, bei dem .