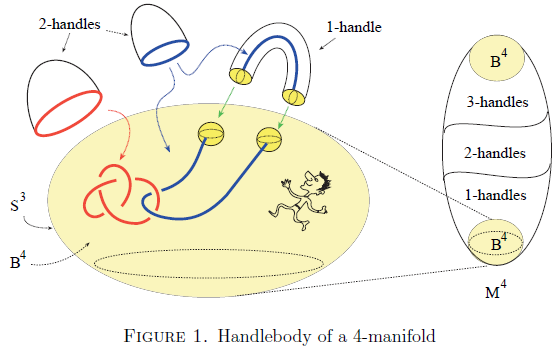
Beschreibung
Eine Henkelzerlegung ist eine Folge von Mannigfaltigkeiten, die durch konsekutives Anhängen von Henkelkörpern auseinander hervorgehen.
Definition
Eine Henkelzerlegung ist eine Folge , wobei aus durch Anhängen von -Henkelkörper hervorgeht.
Eigenschaften
Eigenschaft
Beispiele
-dim Manifolds
Die geschlossenen Vierdimensionalen Mannigfaltigkeiten besitzen eine Henkelkörperstruktur, die mit einer -Sphäre beginnt. An die werden dann , dann , dann -Henkelkörper angehängt. Zuletzt wird die Mannigfaltigkeit mit dem -Henkel geschlossen.
- Die -Henkelkörper haben Füße, die im -dimensionalen Rand wie herausgebohrte Sphären aussehen. Läuft man in diese Sphären hinein, so ist es, als würde man durch ein Wurmloch zu nächsten Sphäre laufen. Das Befestigen von -Henkelkörpern lässt sich auch durch das Bohren eines Loches beschreiben. (Man stelle sich vor, wie man ein Loch durch eine Vollkugel bohrt, um einen Torus zu erhalten). Dies erleichtert das Zeichnen von Diagrammen (sonst können -Henkel durch die Wurmlöcher wandern).
- Die -Henkelkörper haben Füße, die wie verknotete Tori aussehen können. Diese Tori können wie bei der Knotenchirurgie zusätzlich mehrere Dehn-Twist haben.
- Die -Henkelkörper werden dabei eindeutig angehängt.