Dehornoys Ordnung

Beschreibung

Dehornoys Ordnung ist eine Links-Ordnung auf Zopfgruppen

Definition

Dehornoys Ordnung ist durch den Positiver Kegel definiert. Ein Zopf, geschrieben mit den Erzeugern ${\sigma }_1,...,{\sigma }_n$ ist genau dann in $P$, wenn der Erzeuger des kleinsten Index, das im Zopf vorkommt einen positiven Exponenten hat.

Beweis: Die definierte Ordnung wirft eine Menge Fragen zur Wohldefiniertheit auf. (1) Was ist mit Wörtern, die niedrigste Erzeuger mit positiven und negativen Exponenten enthalten? (2) Gibt es Zöpfe, die mit positiven und mit negativen Exponenten geschrieben werden können? Wir stellen erstmal fest, dass durch Anwendung der Gruppenrelationen jedes Vorzeichengemische Zopfwort in ein Wort umgewandelt werden kann, bei dem alle kleinsten Erzeuger entweder positiv oder negativ sind. Das löst (1). Allerdings ist immer noch nicht klar, ob ein Wort nicht in nur positive oder nur negative Exponenten umgewandelt werden kann. Wir entwickeln daher eine geometrische Intuition. Sei $D_n\subseteq \mathbb{C}$ die $n$-fach durchbohrte Kreisscheibe. Die Bohrungen seien entlang $\mathbb{R}$ in Reihe verteilt. Dadurch wird $\mathbb{R}$ in $n+1$ Segmente unterteilt, die wir mit $E_i$ bezeichnen. Wir betrachten nun wie ein Zopf, bestehend aus den Erzeugern ${\sigma }_i$ auf den Segmenten wirkt. Damit können wir dann irgendwie die Positivität ermitteln. Genau verstehe ich es aber noch nicht.

• Beeinflusst ein Erzeuger ein Segment nicht, lassen wir es gerade
• Sonst werden Kurven gezeichnet. Die Kurven sind so, dass sie $\mathbb{R}$ so selten wie möglich schneiden

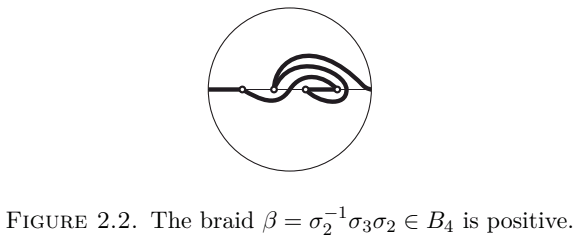Wir stellen fest: Besitzt ein Wort nur positive Erzeuger, so ist das erste gebogene Segment unter $\mathbb{R}$. Besitzt ein Wort nur negative erste Erzeuger, so ist das Segment über $\mathbb{R}$. Daraus folgt, dass Zopfgruppe in zwei Mengen zerlegbar ist $B_n=P\cup \{1\}\cup P^{-1}$. Offensichtlich ist $P$ eine Halbgruppe. Damit sind alle Voraussetzungen erfüllt. $\square$

lit_BasicResultsBraid