Präsentation Symmetrisches Polynom

Beschreibung

Für das Zahlentheorieseminar soll eine Prsentation vrogestellt werden. Ich möchte hier den Ablauf vorstellen.

Ablauf

Ich möchte heute symmetrische Polynome vorstellen. Dazu beginne ich mit einem persönlichen Beispiel, bei denen mir symmetrische Polynome von alleine begegnet sind. Nämlich habe ich mich in den Semesterferien damit beschäftigt, Erweiterung von F2 zu visualisieren und dadurch besser zu verstehen. Bisher konnte ich nur F4 und F8 visualisieren. F4 ist jedoch unkompliziert genug, dass wir die Schritte gemeinsam durchgehen können.

Wie sieht F4 aus? Nun, F4 ist ein Körper mit 4 Elemente auf dem man addieren, multiplizieren, subtrahieren und dividieren kann. Daraus wird häufig der Fehlschuss erstellt, dass F4 dann irgendwie so ungefähr wie Z/4Z ist, schließlich kann man auf Z/4Z auch addieren, multiplizieren und subtrahieren. Dadurch erhaltet ihr aber von mir nur Blicke der Missbilligung. F4 ist mit 4 Elementen sehr leicht vorzustellen und zu verstehen.

Wie kann man ${\text{F}}_4$ definieren? Es gibt viele Charakterisierungen aber ich wähle folgende: Nach Vorlesung sind die Elemente von ${\text{F}}_4$ genau die Nullstellen von $x^4-x=x^4+x=(x^2+x+1)(x+1)x$ in ${\text{F}}_2$ Darunter finden wir die bekannten Elemente $1$ und $0\in {\text{F}}_2$. ${\text{F}}_4$ hat aber $4$ Elemente und damit fehlen uns noch $2$ weitere. Diese sind die Nullstellen des Irreduziblen Polynoms $x^2+x+1$ und offensichtlich nicht $0,1$, denn das sind keine Nullstellen, des oberen Polynoms. Nennen wir daher die beiden Nullstellen ${\alpha }_1,{\alpha }_2$. Welche Eigenschaften können wir den Nullstellen entziehen? Wir könnten erstmal das obere Polynom als Produkt von Linearfaktoren schreiben, erhalten wir: $x^2+x+1=(x-{\alpha }_1)(x-{\alpha }_2)=x^2-({\alpha }_1+{\alpha }_2)x+{\alpha }_1{\alpha }_2$ Wir führen einen Koeffizientenvergleich durch und erhalten: ${\alpha }_1+{\alpha }_2=1,{\alpha }_1{\alpha }_2=1$ D.h. ${\alpha }_1$ ist das multiplikative Inverse von ${\alpha }_2$. Wir wissen auch sofort ${\alpha }_2={\alpha }_1+1$ und ${\alpha }_1={\alpha }_2+1$ Nach ein wenig herumgerechne, worauf ich nicht zu sehr eingehen will, erhalten wir folgendes Diagramm: (Zeige Processing)

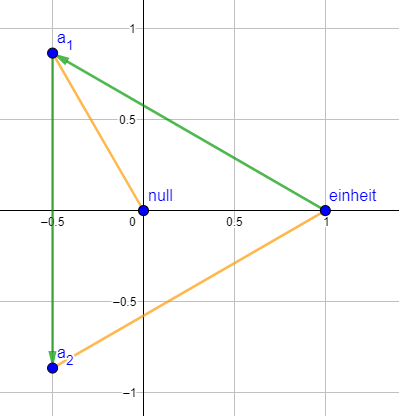
Ich möchte kurz auf eine Eigenart von Nullstellen von irreduziblen Polynomen eingehen. Vielleicht erinnert ihr euch an manche Übungsblätter aus der letzten Vorlesung. Wenn man versucht hat Eigenschaften von Elementen aus Körpererweiterungen zu zeigen, dann war häufig der erste Schritt: Sei $\alpha$ eine Nullstelle des irreduziblen Polynoms (z.B. $x^2+x+1$), dann gelten folgende Eigenschaften. Diese Eigenschaften treffen also auf alle Nullstellen zu, egal, welche man als $\alpha$ bezeichnet. Tatsächlich ist diese Erkenntnis, dass die Nullstellen von irreduziblen Polynomen manchmal ununterscheidbar, sozusagen vertauschbar sind, die Motivation, die die Galoistheorie und die Körperautomorphismen hervorgebracht hat. Ich möchte, dass ihr euch diese Vertauschbarkeit von Nullstellen merkt, da sie heute noch relevant werden könnte.

Führen wir das gleiche mit einem Element aus ${\text{F}}_8$ durch. Ein Element, das in ${\text{F}}_8$ aber nicht im einzigen echten Unterkörper ${\text{F}}_2$ liegt erhält man indem man eine Nullstelle eines irreduziblen Polynoms dritten Grades wählt. Nenne ein irreduzibles Polynom von Grad $3$.

Dann kann man die gleiche Rechung machen: $0,1$ sind keine Nullstellen, also sind die Nullstellen nicht in ${\text{F}}_2$ (sondern in ${\text{F}}_8$), Zerlegung in Linearfaktoren, Koeffizientenvergleich, man erhält drei Gleichungen.

Distanzieren wir uns ein wenig von endichen Körpern und nehmen ein bequemeres Beispiel. Wir führen das gleiche Verfahren nochmal durch. Diesmal benutzen wir ein Polynom von Grad $5$ $f(x)=x^5+a{x}^4+b{x}^3+c{x}^2+dx+e$ in $\mathbb{R}$. Dessen Nullstellen bezeichnen wir mit $x_1$ bis $x_5$. Wir können also $f$ als Linearfaktoren schreiben, ausmultiplizieren und erhalten durch Koeffizientenvergleich die Gleichungen …

Wir könnten also die Parameter eines Polynoms aus den Nullstellen berechnen, indem wir die Nullstellen in diese rechte Seite der Gleichung berechnen. Dieses Vorgehen ist sehr, sehr einfach, wenn man es mit den Formeln vergleicht, mit denen man rückwärts die Nullstellen aus den Parametern berechnet. Versuchen wir die rechte Seite ein wenig zu strukturieren, damit wir leichter Parameter aus Nullstellen erhalten können. Wir bemerken, dass die rechte Seite der Gleichung wie ein Polynom in mehreren Variablen aussieht. (geschrieben $p(x_1,...,x_n)$) Wir bezeichnen diese Polynome als die Elementarsymmetrischen Polynome. In diesen Polynomen erkennen wir eine gewisse Struktur. Sie sind Summen vossn Produkten, die sich aus immer gleich vielen verschiedenen Faktoren zusammensetzen. Wir erkennen des Weiteren, dass alle Kombinationen aus k Faktoren vorhanden sind. Je nachdem wie viele Faktoren jeder Summand hat bezeichnen wir die elementarsymmetrichen Polynome mit $s_k(x_1,...,x_n)$. Wir können die rechte Seite dieser Gleichungen schreiben als ${\sum }_{\{i_1,...,i_k\}\subseteq \{0,...,5\}}{X}_{i_1}...X_{i_k}$ oder auch als

${\sum }_{1\le i_1\le ...\le i_k\le n}{X}_{i_1}...X_{i_k}$

Diese Polynome haben die Eigenschaft, dass sie Symmetrisch bezüglich ihrer Variablen sind.

Erinnert euch daran, wie ich vorhin von vertauschbaren Nullstellen gesprochen habe. Ebenso können wir hier $x_i,x_j$ vertauschen und wir erhalten den gleichen Term. Zum Beispiel Vertauschen wir $x_1$ und $x_2$ in $s_2(x_1,...,x_5)$, wir erhalten den gleichen Term. Oder etwas konkreter. Wenn wir beliebige Eingaben wählen, dann gilt z.B. $s_2(1,2,3,3,7)=s_2(2,1,3,3,7)$. Ich nehme an, hier sind hauptsächlich Lehramtsstudierende. In dem Fall sollte bekannt sein, welches Wort in der Didaktik verwendet wird, wenn eine Figur unter einer Kongruenzabbildung gleich bleibt.

Bei einer Kongruenzabbildung werden Punkte vertauscht und die Figur bleibt gleich. Hier vertauschen wir Parameter und der Funktionsterm bleibt gleich. Funktionen mit dieser Eigenschaft werden als Symmetrische Funktion bezeichnet. Heute werden wir nur Polynome behandeln und daher das Wort Symmetrische Polynome verwenden.

Das Wort symmetrisch ist aus anderem Grund passend gewählt, denn skizziert man den Graph einer elementarsymmetrischen Funktionen. beispielsweise $s_2(x_1,x_2)=x_1{x}_2$, dann sieht man, dass dieser achsensymmetrisch bezüglich der Winkelhalbierenden der $x_1$ und $x_2$-Achse ist. Das gleiche Verhalten zeigt auch $s_1(x_1,x_2)=x_1+x_2$.

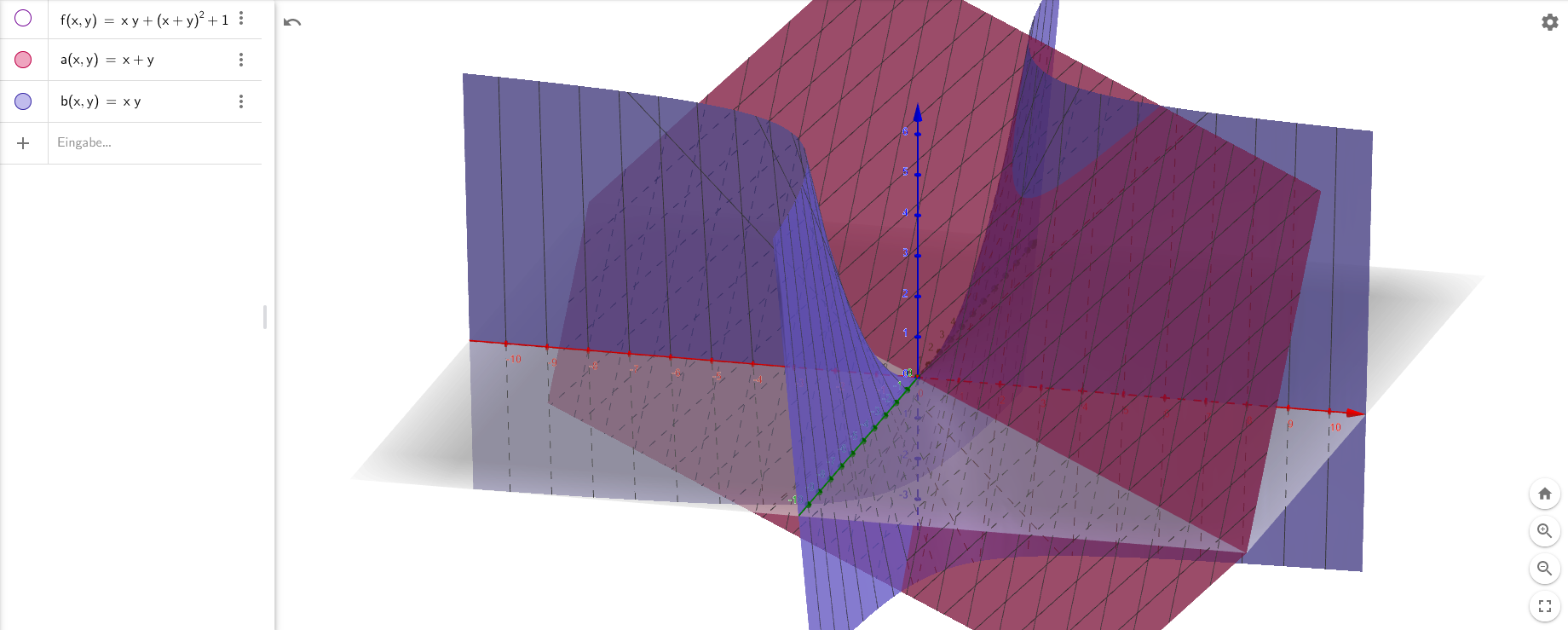
Wenn man beide Graphen skizziert, können wir gleich eine Vermutung anstellen. Beide Graphen haben an zueinander Achsensymmetrischen Punkten den gleichen Wert. Wenn wir diese Graphen also addieren bzw. subtrahieren, dann erhalten wir wieder einen symmetrischen Graphen. Mit der gleichen Argumentation können wir die Werte von zwei Graphen folgendermaßen miteinander multiplizieren und wir erhalten wieder einen symmetrischen Graphen. Ebenso können wir Konstanten addieren oder mit Konstanten skalieren und die Funktion bleibt symmetrisch. Das Vorgehen lässt sich leicht auf Polynome mit mehr als 2 Variablen verallgemeinern.

Eine Summe, Differenz oder Produkt von zwei symmetrischen Polynomen ergibt wieder ein symmetrisches Polynom. An welche algebraische Struktur erinnert das? Was ist das Eins und Null Element?

Wir können also symmetrische Polynome erzeugen, indem wir Polynome aus Elementarsymmetrischen Polynomen bilden. Zum Beispiel: $s_1^2+2s_1+s_0=(x_1+x_2{)}^2+2(x_1+x_2)+(x_1{x}_2)$ (mit Graphen)

Das wirft aber die Frage auf: Gibt es symmetrische Polynome, die nicht als Polynom von Elementarsymmetrischen Polynomen geschrieben werden kann? Oder äquivalent dazu: Kann jedes Symmetrische Polynom als Polynom von Elementarsymmetrischen Polynomen geschrieben werden?

\newcommand{\R}{\mathbb R}

lit_hadlockFieldTheoryIts2000