Beschreibung
Das Differentialfunktional interpretiert das aus der üblichen Ableitung als ein Funktional, der auf Differentialformen operiert.
Definition
Es gibt auf dem Raum der Differentialform eine eindeutige lineare Abbildung die eindeutig durch folgende Eigenschaften bestimmt ist:
- Für ein beliebiges ist das übliche Differential einer Mannigfaltigkeitenfunktion.
- Für ein gilt
Für eine Karte Differentialform definieren wir als
Motivation
ist einfach eine Skalarfunktion. Nimmt man das Differential davon, erhält man eine -Form-Funktion. Dieses keilen wir nun an unsere Basis an.
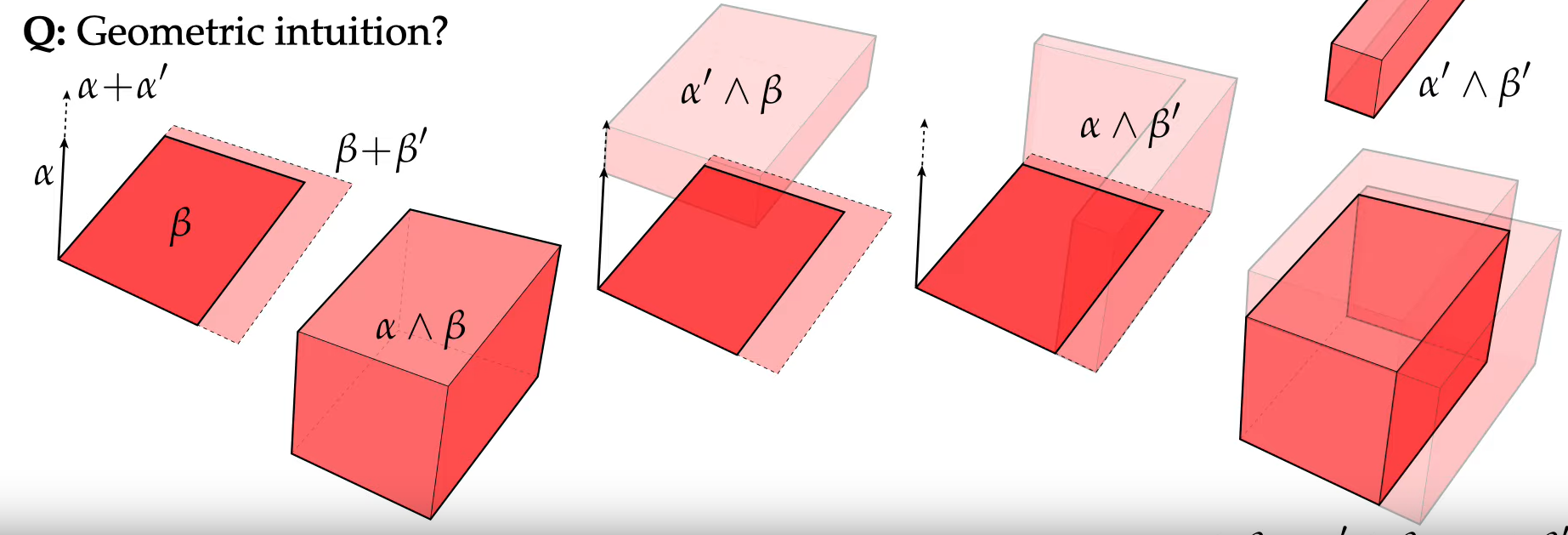
Die Motivation der zweiten Regel ist ganz ähnlich der Motivation der Produktregel (Ableitung) in der Ableitung:
Die dritte Regel ähnelt sehr der Tatasache, dass der Rotor (Lineare Algebra) des Gradient überall ist. Es ähnelt außerdem der Tatsache, dass der Rand eines Randes eines Objektes leer ist.
Eigenschaften
Erkennung von Löchern
Ist eine Differentialform exakt , d.h. ein Differentialfunktional so ist die Form closed. Gild der Kehrsatz, so besitzt die beobachtete Mannigfaltigkeit keine Löcher.
Beispiele
Äußeres Differential von Skalarfunktionen
Sei ein Skalarfeld. Dann gibt punkteweise den Kovektor zum Gradienten an.
Es gibt einen weiteren Unterschied zwischen dem Differential und dem Gradienten. Der Gradient benötigt ein Skalarprodukt für seine Definition. Der Gradient ist also von der Wahl des Skalarprodukt abhängig. Das Differential nicht